
【题目】如图,AE⊥BD于E,CF⊥BD于F,AB=CD,AE=CF,则图中全等三角形共有( )
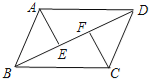
A.1对B.2对C.3对D.4对
【答案】C
【解析】
试题由于AE⊥BD于E,CF⊥BD于F得到∠AEB=∠CFD=90°,则可根据“HL”证明出Rt△ABE≌Rt△CDF,根据全等的选择得BE=DF,∠ABE=∠CDF,于是利用“SAS“可证明
△AED≌△CFB,则有AD=CB,所以利用”SSS”证明△ABD≌△CDB.
解:∵AE⊥BD于E,CF⊥BD于F,
∴∠AEB=∠CFD=90°,
在Rt△ABE和Rt△CDF中,
![]() ,
,
∴Rt△ABE≌Rt△CDF(HL),
∴BE=DF,∠ABE=∠CDF,
∴DE=BF,
同样可利用“SAS”证明△AED≌△CFB,
∴AD=BC,
∴可利用”SSS”证明△ABD≌△CDB.
故选C.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】某市教育行政部门为了了解初一学生每学期参加综合实践活动的情况,随机抽样调查了某校初一学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图(如图)
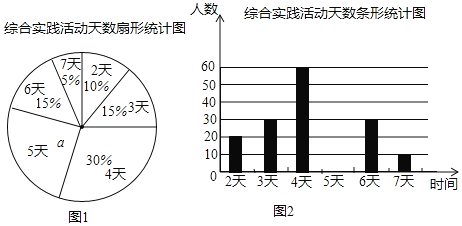
请你根据图中提供的信息,回答下列问题:
(1)扇形统计图中a的值为 ,“活动时间为4天”的扇形所对圆心角的度数为 °,该校初一学生的总人数为 ;
(2)补全频数分布直方图;
(3)如果该市共有初一学生6000人,请你估计“活动时间不少于4天”的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队接到任务通知,需要修建一段长1800米的道路,按原计划完成总任务的![]() 后,为了让道路尽快投入使用,工程队将工作效率提高了50%,一共用了10小时完成任务.
后,为了让道路尽快投入使用,工程队将工作效率提高了50%,一共用了10小时完成任务.
(1)按原计划完成总任务的![]() 时,已修建道路多少米?
时,已修建道路多少米?
(2)求原计划每小时修建道路多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,梯形AOCD中,AD=9,OC=10,AO=4,在线段OC上任取一点N(不与O,C重合),连接DN,作NE⊥DN,交AO于点E.

(1)当CN=2时,求点E的坐标.
(2)若CN=x,OE=y,求y与x的函数关系式.
(3)探索与研究:若点M从O点沿OC方向、N点从C点沿CO方向同时等速运动,现有一点F,满足MF⊥MN,NF⊥ND.
①猜想F点在什么线上运动?并求出这条线所对应的函数关系式,并写出自变量的取值范围;
②求出F点在运动过程中的最高点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知EF//AD,∠1=∠2,∠BAC=70o.将求∠AGD的过程填写完整.

解:![]() ,
,
![]() ________( )
________( )
又![]() ,
,
![]() ( )
( )
![]() ( )
( )
![]() ________
________ ![]() ( )
( )
又![]() ,
,
![]() ________
________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景
在数学活动课上,张老师要求同学们拿两张大小不同的矩形纸片进行旋转变换探究活动.如图 1,在矩形纸片ABCD 和矩形纸片EFGH中,AB=1,AD=2,且FE>AD,FG>AB,点E 是 AD 的中点,矩形纸片 EFGH 以点E 为旋转中心进行逆时针旋转,在旋转过程中会产生怎样的数量关系,提出恰当的数学问题并加以解决.
解决问题
下面是三个学习小组提出的数学问题,请你解决这些问题.
(1)“奋进”小组提出的问题是:如图 1,当 EF 与 AB 相交于点 M,EH 与 BC 相交于点 N 时,求证:EM=EN.
(2)“雄鹰”小组提出的问题是:在(1)的条件下,当 AM=CN 时,AM 与 BM 有怎样的数量关系,请说明理由.
(3)“创新”小组提出的问题是:若矩形 EFGH 继续以点 E 为旋转中心进行逆时针旋转,当 ![]() 时,请你在图 2 中画出旋转后的示意图,并求出此时 EF 将边 BC 分成的两条线段的长度.
时,请你在图 2 中画出旋转后的示意图,并求出此时 EF 将边 BC 分成的两条线段的长度.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,点
,点![]() .
.
(1)只用直尺(没有刻度)和圆规,求作一个点P,使点P同时满足下列两个条件
①点P到A,B两点的距离相等;
②点P到![]() 的两边的距离相等.
的两边的距离相等.
(要求保留作图痕迹,不必写出作法)
(2)在(1)作出点P后,点P的坐标为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中装有8个红球和16个白球,它们除颜色不同外其余都相同.
(1)求从布袋中摸出一个球是红球的概率;
(2)现从布袋中取走若干个白球,并放入相同数目的红球,搅拌均匀后,再从布袋中摸出一个球是红球的概率是![]() ,问取走了多少个白球?
,问取走了多少个白球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com