
【题目】为发展学生的数学核心素养,培养学生的综合能力,某市开展了初三学生的数学学业水平测试.在这次测试中,从甲、乙两校各随机抽取了30名学生的测试成绩进行调查分析.(说明:成绩80分及以上为优秀,60~79分为合格,60分以下为不合格)
收集数据:
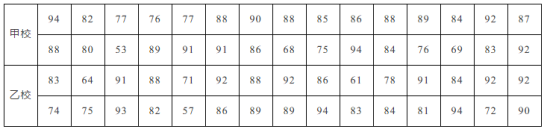
整理、描述数据:
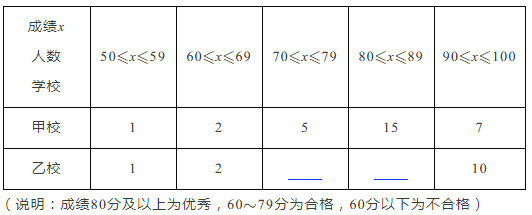
分析数据:
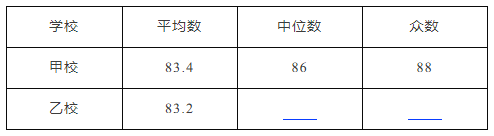
(1)请你补全表格;
(2)若甲校有300名学生参加测试,请估计甲校此次测试的优秀人数约为多少;
(3)利用表2的数据,请你对甲乙两所学校的测试成绩进行评价.
【答案】(1)5,12;86,92;(2)220名;(3)从平均数来看,甲校的平均分比乙校的平均分高,甲校的成绩比较好;从众数看,乙校的众数比甲校的众数高,乙校的成绩较好
【解析】
(1)利用分析数据的方法以及中位数,众数的定义解决问题即可.
(2)利用样本估计总体的思想解决问题即可.
(3)根据平均分,众数分别进行判断即可.
(1)由题可知:乙校在70≤x<79的人数有5人,80≤x<89的人数有12人,
乙校的中位数为86,众数为92.
故答案为:5,12;86,92.
(2)![]() (名)
(名)
答:估计甲校此次测试的优秀人数为220名.
(3)从平均数来看,甲校的平均分比乙校的平均分高,甲校的成绩比较好;
从众数看,乙校的众数比甲校的众数高,乙校的成绩较好.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.

(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C作△ABC外接圆⊙O的切线交AB的垂直平分线于点D,AB的垂直平分线交AC于点E.若OE=2,AB=8,则CD=_____.
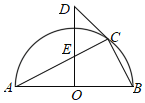
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() 中,
中,![]() ,P是斜边AC上一个动点,以即为直径作
,P是斜边AC上一个动点,以即为直径作![]() 交BC于点D,与AC的另一个交点E,连接DE.
交BC于点D,与AC的另一个交点E,连接DE.
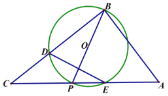
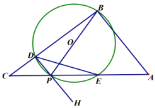
(1)当![]() 时,
时,
①若![]() ,求
,求![]() 的度数;
的度数;
②求证![]() ;
;
(2)当![]() ,
,![]() 时,
时,
①是含存在点P,使得![]() 是等腰三角形,若存在求出所有符合条件的CP的长;
是等腰三角形,若存在求出所有符合条件的CP的长;
②以D为端点过P作射线DH,作点O关于DE的对称点Q恰好落在![]() 内,则CP的取值范围为________.(直接写出结果)
内,则CP的取值范围为________.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国魏晋时期的数学家刘徽首创“割圆术”,提出圆内接正多边形边数无限增加时,周长就越接近圆周长,由此求得圆周率π的近似值.如图,设半径为r的内接正n边形的周长为C,圆的直径为d,则π≈![]() .例如,当n=6时,π
.例如,当n=6时,π![]() ,则当n=12时,π的值约为( )(参考数据:sin15°=cos75°≈0.26)
,则当n=12时,π的值约为( )(参考数据:sin15°=cos75°≈0.26)
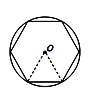
A.3.11B.3.12C.3.13D.3.14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-2,与x轴的一个交点在(-3,0)和(-4,0)之间,其部分图象如图所示.则下列结论:①4a-b=0;②c<0;③-3a+c>0;④4a-2b>at2+bt(t为实数);⑤点![]() ,
,![]() ,
,![]() 是该抛物线上的点,则y1<y2<y3.其中正确结论的个数是( )
是该抛物线上的点,则y1<y2<y3.其中正确结论的个数是( )
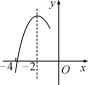
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
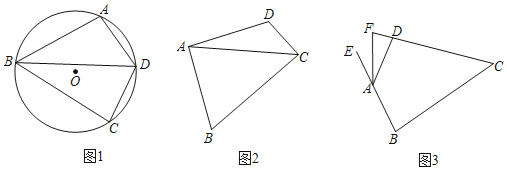
【题目】定义:有一组邻边相等且对角互补的四边形叫做等补四边形.
理解:
![]() 如图1,点
如图1,点![]() 在
在![]() 上,
上,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,连接
,连接![]() 求证:四边形
求证:四边形![]() 是等补四边形;
是等补四边形;
探究:
![]() 如图2,在等补四边形
如图2,在等补四边形![]() 中
中![]() 连接
连接![]() 是否平分
是否平分![]() 请说明理由.
请说明理由.
运用:
![]() 如图3,在等补四边形
如图3,在等补四边形![]() 中,
中,![]() ,其外角
,其外角![]() 的平分线交
的平分线交![]() 的延长线于点
的延长线于点![]() 求
求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
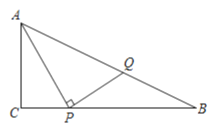
【题目】如图,![]() 中,
中,![]() ,
,![]() 是
是![]() 边上一动点,连接
边上一动点,连接![]() ,作
,作![]() 交
交![]() 于
于![]() ,已知
,已知![]() ,
,![]() ,设
,设![]() 的长度为
的长度为![]() ,
,![]() 的长度为
的长度为![]() .
.
小青同学根据学习函数的经验对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
下面是小青同学的探究过程,请补充完整:
(1)按照下表中自变量![]() 的值进行取点、画图、测量,分别得到了
的值进行取点、画图、测量,分别得到了![]() 的几组对应值:
的几组对应值:
| 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 6 |
| 0 | 1.56 | 2.24 | 2.51 |
| 2.45 | 2.24 | 1.96 | 1.63 | 1.26 | 0.86 | 0 |
(说明:补全表格时相关数据保留一位小数)
![]() 的值约为__________
的值约为__________![]() ;
;
(2)在平面直角坐标系中,描出已补全后的表格中各组数值所对应的点![]() ,画出该函数的图象;
,画出该函数的图象;
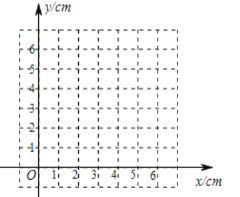
(3)结合画出的函数图象,解决问题:
①当![]() 时,对应的
时,对应的![]() 的取值范围约是_____________;
的取值范围约是_____________;
②若点![]() 不与
不与![]() ,
,![]() 两点重合,是否存在点
两点重合,是否存在点![]() ,使得
,使得![]() ?________________(填“存在”或“不存在”)
?________________(填“存在”或“不存在”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() 点
点![]() 与点
与点![]() 在
在![]() 的同侧,且
的同侧,且![]() .
.

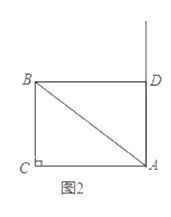
(1)如图1,点![]() 不与点
不与点![]() 重合,连结
重合,连结![]() 交
交![]() 于点
于点![]() .设
.设![]() 求
求![]() 关于
关于![]() 的函数解析式,写出自变量
的函数解析式,写出自变量![]() 的取值范围;
的取值范围;
(2)是否存在点![]() ,使
,使![]() 与
与![]() 相似,若存在,求
相似,若存在,求![]() 的长;若不存在,请说明理由;
的长;若不存在,请说明理由;
(3)如图2,过点![]() 作
作![]() 垂足为
垂足为![]() .将以点
.将以点![]() 为圆心,
为圆心,![]() 为半径的圆记为
为半径的圆记为![]() .若点
.若点![]() 到
到![]() 上点的距离的最小值为
上点的距离的最小值为![]() ,求
,求![]() 的半径.
的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com