
【题目】如图1,四边形OABC是菱形,点C在x轴上,AB交y轴于点H,AC交y轴于点M.已知点A(-3,4).
(1)求AO的长;
(2)求直线AC的解析式和点M的坐标;
(3)如图2,点P从点A出发,以每秒2个单位的速度沿折线A-B-C运动,到达点C终止.设点P的运动时间为t秒,△PMB的面积为S.
①求S与t的函数关系式;
②求S的最大值.
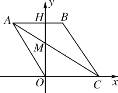
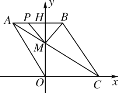
图1 图2
【答案】(1)5;(2)y=-![]() x+
x+![]() ,M(0,
,M(0,![]() );(3)①S=
);(3)①S=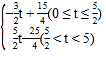 ;②
;②![]() .
.
【解析】
(1)根据A的坐标求出AH、OH,根据勾股定理求出即可;
(2)根据菱形性质求出B、C的坐标,设直线AC的解析式是y=kx+b,把A(-3,4),C(5,0)代入得到方程组,求出即可;
(3)①过M作MN⊥BC于N,根据角平分线性质求出MN,P在AB上,根据三角形面积公式求出即可;P在BC上,根据三角形面积公式求出即可;②求出P在AB的最大值和P在BC上的最大值比较即可得到答案.
(1)∵A(-3,4),
∴AH=3,OH=4,
由勾股定理得:AO=![]() =5;
=5;
(2)∵四边形OABC是菱形,
∴OA=OC=BC=AB=5,
5-3=2,
∴B(2,4),C(5,0),
设直线AC的解析式是y=kx+b,
把A(-3,4),C(5,0)代入得:![]() ,
,
解得: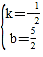 ,
,
∴直线AC的解析式为y=-![]() x+
x+![]() ,
,
当x=0时,y=2.5,
∴M(0,2.5);
(3)①过M作MN⊥BC于N,
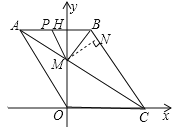
∵四边形OABC是菱形,
∴∠BCA=∠OCA,
∵MO⊥CO,MN⊥BC,
∴OM=MN,
当0≤t<2.5时,P在AB上,MH=4-2.5=![]() ,
,
=![]() ×BP×MH=
×BP×MH=![]() ×(5-2t)×
×(5-2t)×![]() =-
=-![]() t+
t+![]() ,
,
∴S=![]() t+
t+![]() ,
,
当t=2.5时,P与B重合,△PMB不存在;
当2.5<t≤5时,P在BC上,S=![]() ×PB×MN=
×PB×MN=![]() ×(2t-5)×
×(2t-5)×![]() =
=![]() t-
t-![]() ,
,
∴S=![]() t
t![]() ,
,
故S=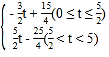 ;
;
②当P在AB上时,高MH一定,只有BP取最大值即可,即P与A重合,S最大是![]() ×5×
×5×![]() =
=![]() ,
,
同理在BC上时,P与C重合时,S最大是![]() ×5×
×5×![]() =
=![]() ,
,
∴S的最大值是![]() .
.


科目:初中数学 来源: 题型:
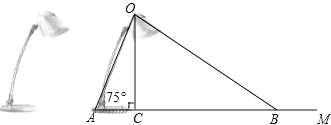
【题目】如图为放置在水平桌面上的台灯的平面示意图,灯臂AO长为40cm,与水平面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°,求该台灯照亮水平面的宽度BC(不考虑其他因素,结果精确到0.1cm.温馨提示:sin75°≈0.97,cos75°≈0.26, ![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
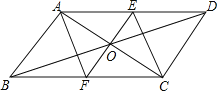
【题目】如图:在平行四边形ABCD中,对角线AC与BD交于点O,过点O的直线EF分别与AD、BC交于点E、F,EF⊥AC,连结AF、CE.
(1)求证:OE=OF;
(2)请判断四边形AECF是什么特殊四边形,请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点称为格点,以格点为顶点的多边形称为格点多边形.设格点多边形的面积为S,该多边形各边上的格点个数之和为m,内部的格点个数为n,试探究S与m、n之间的关系式.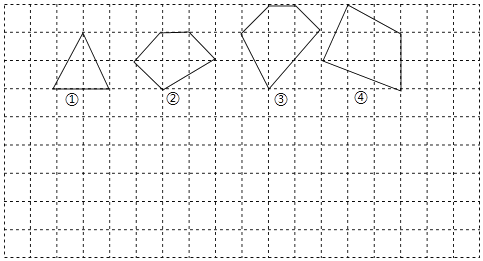
(1)根据图中提供的信息填表:
格点多边形各边上的 | 格点边多边形内部的 | 格点多边形的面积 | |
多边形1 | 4 | 1 | 2 |
多边形2 | 5 | 2 | ② |
多边形3 | 6 | 3 | 5 |
多边形4 | ① | 4 |
|
一般格点多边形 | m | n | S |
则S=(用含m、n的代数式表示)
(2)对正三角形网格中的类似问题进行探究:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,如图1、2是该正三角形格点中的两个多边形:设格点多边形的面积为S,该多边形各边上的格点个数之和为m,内部的格点个数为n,试探究S与m、n之间的关系式.则S与m、n之间的关系为S=(用含m、n的代数式表示).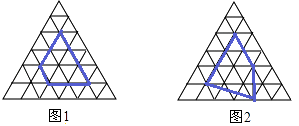
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1计算:![]() ;
;
(2)解不等式组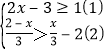
请结合题意填空,完成本题的解答:
解不等式(1),得______________.
解不等式(2),得_______________.
把不等式(1)和(2)的解集在数轴上表示出来
![]()
∴原不等式组的解集为_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A, D1,D三点的坐标分别是(0,4),(0,3),(0,2).

(1)对称中心的坐标;
(2)写出顶点B, C, B1 , C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD∥BC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E,试说明AB∥DC,把下面的说理过程补充完整.
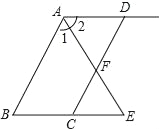
证明:∵AD∥BC(已知)
∴∠2=∠E(___________________________)
∵AE平分∠BAD(已知)
∴∠1=∠2 (_________________________)
∴∠1=∠E(___________________________)
∵∠CFE=∠E(已知)
∴∠1=∠______(______________________)
∴AB∥CD(_________________________________)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com