练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．已知不等式3（2x-a）＜2（x+2a）与6（x-a）＜4（x+a）同解，求a的值．

    分析 先用到a表示出两个不等式的解集，根据两不等式的解集相同即可得出结论．

    解答 解：解不等式3（2x-a）＜2（x+2a）可得：x$＜\frac{7}{4}a$，
    解不等式6（x-a）＜4（x+a）可得：x＜5a，
    因为不等式3（2x-a）＜2（x+2a）与6（x-a）＜4（x+a）同解，
    所以可得：$\frac{7}{4}a=5a$，
    解得：a=0．

    点评 本题考查的是解一元一次不等式，熟知去分母，去括号，移项，合并同类项，化系数为1是解一元一次不等式的基本步骤是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    9．如图，菱形ABCD的边长为4，且∠ABC=60°，点E是CD的中点，点M为AC上一点，求MD+ME的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．已知抛物线如图所示．
    （1）求抛物线的解析式及抛物线顶点M的坐标；
    （2）若点N为线段BM上一点，过点N作x轴的垂线，垂足为点Q，当点N在线段BM上运动时（点N不与点B、点M重合），设OQ的长为t，四边形NQAC的面积为S，求S与t之间的函数关系式及自变量t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

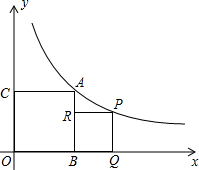    7．如图，双曲线y=$\frac{k}{x}$（x＞0）在第一象限内的一支，点A，P是图象上的两点，作AB⊥x轴，AC⊥y轴，PQ⊥x轴，PR⊥AB，垂足分别是B，C，Q，R，且四边形ABOC与四边形PQBR都是正方形．
    （1）当k=1时，求正方形ABOC与正方形PQBR的边长；
    （2）当k=2时，求正方形ABOC与正方形PQBR的边长；
    （3）试求出第（1），（2）题中的正方形ABOC与正方形PQBR的边长之比，你发现其比有何特征？再请你探索一下，对于任意的k（k＞0）你所发现的特征是否还成立？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．已知144x2-49=0，27y3+1000=0，且xy＜0，求x+y，xy的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

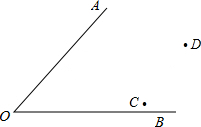    4．OA、OB为两条笔直的公路，C、D为两个工厂，现欲在附近建一个货运站，使得它到两条公路距离相等，到两家工厂距离也相等．请作出符合条件的货运站P．不写作法，保留作图痕迹．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图1，在菱形ABCD中，AB=2，∠BAD=60°，对角线AC、BD相交于点M，点O是边AD的中点．
    （1）求对角线AC、BD的长；
    （2）设∠COD=α，∠OCD=β，则sinα与sinβ之间有何关系，并说明理由；
    （3）如图2，以AD、OB所在直线为x、y轴，建立如图直角坐标系，在y轴上是否存在一点P，使△PAC为直角三角形？若存在，请直接写出点P坐标；若不存在，说明理由．

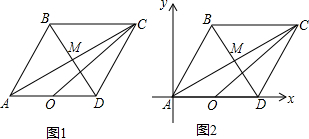
    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．如图1，将两个等腰直角三角形纸片ABC和DEC的顶点C重合放置，点D和E分别在边AC和BC上，其中∠C=90°，AC=BC，DC=EC．
    操作发现：如图2，固定△ABC，使△DEC绕点C顺时针旋转45°，点D恰好落在AB边上，填空：
    ①线段DE与AC的位置关系是平行；
    ②设△BDC的面积为S1，△AEC的面积为S2，则S1与S2的数量关系是相等．

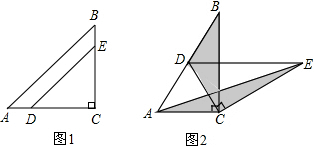
    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．瑞安市村村开展“建设生态宜居环境，打造绿色秀美乡村”活动，某村计划哟个6800元资金购买甲，乙，丙三种树的单价分别是200元，300元，500元．
    （1）若购买甲种树的棵树是乙种树的2倍，恰好用完计划资金．
    ①设购买乙种树x棵，丙种树y棵，根据题意，完成以下表格：
     甲种树乙种树丙种树总数
    三种树的棵树2x xy20
    三种树的金额400x300x500y 6800
    ②求这三种树各能购买多少棵？
    （2）若又增加了1200元的购树款，在购买总棵树数不变的前提下，并将购树款恰好用完，求这三种树有哪些购买方案？请说明理由．

    查看答案和解析>>

    同步练习册答案