
【题目】已知:抛物线y=ax2﹣3ax+4与x轴交于A、B两点(点A在点B的左侧),且AB=5.
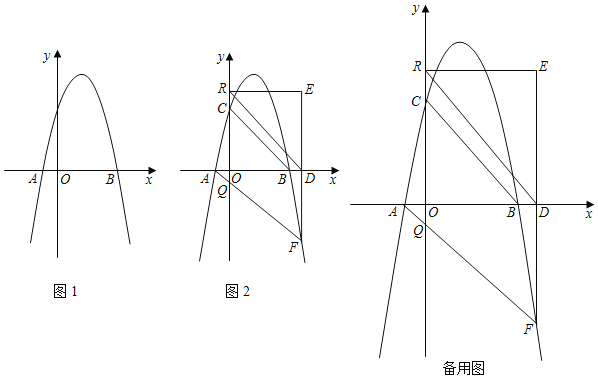
(1)如图1,求抛物线的解析式;
(2)如图2,抛物线与y轴交于点C,F是第四象限抛物线上一点,FD⊥x轴,垂足为D,E是FD延长线上一点,ER⊥y轴,垂足为R,FA交y轴于点Q,若BC∥RD.求证:OQ=CR;
(3)在(2)的条件下,在RD上取一点M,延长OM交线段DE于点N,RE交抛物线于点T(点T在抛物线对称轴的右侧),连接MT、NT,且TM⊥OM,![]() =
=![]() ,H是AF上一点,当∠DHF=135°时,求点H的坐标.
,H是AF上一点,当∠DHF=135°时,求点H的坐标.
【答案】(1)y=﹣x2+3x+4;(2)见解析;(3)点H(![]() ,﹣
,﹣![]() )
)
【解析】
y=ax2﹣3ax+4的对称轴为x=﹣![]() =
=![]() ,且AB=5,得到OB、OA的长度,再到点A点C的坐标,从而求出抛物线解析式.
,且AB=5,得到OB、OA的长度,再到点A点C的坐标,从而求出抛物线解析式.
设点F(m,﹣m2+3m+4),由 BC∥RD 和OQ∥DF,找到△AOQ∽△ADF,得出OQ=OR.
点M作MG⊥OR,MP⊥RE,过点D作DK⊥AF,过点O作WO⊥ON,交ER的延长线于W,证明△MGO≌△MPT,再设设RM=4![]() t,TN=5t,△WRO≌△NDO和△WTO≌△NTO,最后根据勾股定理和三角函数求解即可.
t,TN=5t,△WRO≌△NDO和△WTO≌△NTO,最后根据勾股定理和三角函数求解即可.
(1)∵抛物线y=ax2﹣3ax+4的对称轴为x=﹣![]() =
=![]() ,且AB=5,
,且AB=5,
∴OB=![]() =4,OA=
=4,OA=![]() ﹣
﹣![]() =1,
=1,
∴点A(﹣1,0),点C(4,0),
∴0=a+3a+4,
∴a=﹣1,
∴抛物线y=﹣x2+3x+4;
(2)设点F(m,﹣m2+3m+4)
∴OD=m,DF=m2﹣3m﹣4,
∵抛物线y=﹣x2+3x+4与y轴交于点C,
∴点C(0,4),
∴OB=OC=4,
∵BC∥RD,
∴![]() ,
,
∴OR=OD=m﹣4,
∵OQ∥DF,
∴△AOQ∽△ADF,
∴![]() ,
,
∴![]()
∴OQ=m﹣4,
∴OQ=OR;
(3)如图,过点M作MG⊥OR,MP⊥RE,过点D作DK⊥AF,过点O作WO⊥ON,交ER的延长线于W,
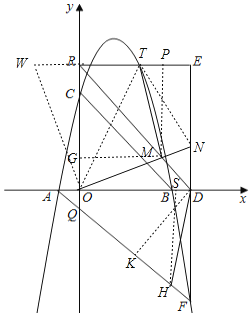
∵∠ORD=45°=![]() ∠ERO,
∠ERO,
∴∠ERD=∠ORD,且MG⊥OR,MP⊥RE,
∴MG=MP,
∵∠GMP=∠TMO=90°,
∴∠GMO=∠PMT,且GM=MP,∠MGO=∠MPT=90°,
∴△MGO≌△MPT(AAS)
∴OG=PT,MO=MT,
∵TM⊥ON,
∴∠TOM=45°,
∵RO=RG+GO=RG+(RP﹣RT)=![]() RM+(
RM+(![]() RM﹣RT)
RM﹣RT)
∴RO+RT=![]() RM,
RM,
∵![]() =
=![]() ,
,
∴设RM=4![]() t,TN=5t,
t,TN=5t,
∴RO+RT=8t,
∵∠WON=∠ROD,
∴∠WOR=∠NOD,且RO=OD,∠WRO=∠NDO,
∴△WRO≌△NDO(ASA)
∴WO=NO,WR=DN,
∵∠TON=∠TOW=45°,OT=OT,WO=NO,
∴△WTO≌△NTO(SAS)
∴WT=NT,
∴RT+WR=RT+ND=TN=5t,
∴EN=ED﹣ND=RO﹣(5t﹣RT)=RO+RT﹣5t=8t﹣5t=3t,
∴ET=![]() =
=![]() =4t,
=4t,
∴RO=8t﹣RT=4t+RT,
∴RT=2t,RO=6t,
∴T(2t,6t)
∴6t=﹣4t2+6t+4;
∴t=1或t=﹣1(舍去)
∴RC=2=OQ,
∴AQ=![]() =
=![]() =
=![]()
∴tan∠QAO=![]() =2,
=2,
∵∠DHF=135°,
∴∠DHK=45°,且DK⊥AF,
∴∠DHK=∠KDH=45°,
∴DK=KH,
∵sin∠DAK=![]() =
=![]() ,
,
∴DK=7×![]() =
=![]()
∴tan∠QAO=![]() =2
=2
∴AK=![]()
∴AH=![]() ,
,
∵sin∠QAO=![]() =
=![]() =
=![]() ,
,
∴HS=![]() ,
,
∵tan∠QAO=![]()
∴AS=![]() ,
,
∴OS=![]() ,
,
∴点H(![]() ,﹣
,﹣![]() )
)


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△OA1B1是等边三角形,点B1的坐标是(2,0),反比例函数y=![]() 的图象经过点A1.
的图象经过点A1.
(1)求反比例函数的解析式.
(2)如图,以B1为顶点作等边三角形B1A2B2,使点B2在x轴上,点A2在反比例函数y=![]() 的图象上.若要使点B2在反比例函数y=
的图象上.若要使点B2在反比例函数y=![]() 的图象上,需将△B1A2B2向上平移多少个单位长度?
的图象上,需将△B1A2B2向上平移多少个单位长度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是![]() 的直径,点P在BA的延长线上,PD切
的直径,点P在BA的延长线上,PD切![]() 于点D,过点B作
于点D,过点B作![]() ,交PD的延长线于点C,连接AD并延长,交BE于点E.
,交PD的延长线于点C,连接AD并延长,交BE于点E.
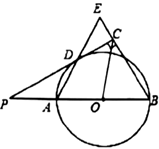
(Ⅰ)求证:AB=BE;
(Ⅱ)连结OC,如果PD=2![]() ,∠ABC=60°,求OC的长.
,∠ABC=60°,求OC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接“六一”儿童节,某儿童品牌玩具专卖店购进了A、B两种玩具,其中A类玩具的进价比B玩具的进价每个多3元,经调查:用900元购进A类玩具的数量与用750元购进B类玩具的数量相同
(1)求A、B两类玩具的进价分别是每个多少元?
(2)该玩具店共购进了A、B两类玩具共100个,若玩具店将每个A类玩具定价为30元出售,每个B类玩具定价25元出售,且全部售出后所获得利润不少于1080元,则商店至少购进A类玩具多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=45°,点D在AB上,点E在AC的延长线上,ED⊥AB,ED交BC于点F,AB=DF,3DF=5EF,CF=l,则AC=_____.
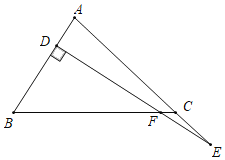
查看答案和解析>>
科目:初中数学 来源: 题型:
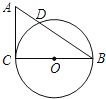
【题目】如图,在Rt△ACB中,∠C=90°,AC=3cm,BC=4cm,以BC为直径作⊙O交AB于点D.
(1)求线段AD的长度;
(2)点E是线段AC上的一点,试问:当点E在什么位置时,直线ED与⊙O相切?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() ,点
,点![]() 是射线
是射线![]() 上一动点,以
上一动点,以![]() 为边向右侧作等边
为边向右侧作等边![]() ,点
,点![]() 的位置随点
的位置随点![]() 的位置变化而变化.
的位置变化而变化.
(1)如图1,当点![]() 在菱形
在菱形![]() 内部或边上时,连接
内部或边上时,连接![]() ,
,![]() 与
与![]() 的数量关系是 ,
的数量关系是 ,![]() 与
与![]() 的位置关系是 ;
的位置关系是 ;
(2)当点![]() 在菱形
在菱形![]() 外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,
外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,
请说明理由(选择图2,图3中的一种情况予以证明或说理).
(3) 如图4,当点![]() 在线段
在线段![]() 的延长线上时,连接
的延长线上时,连接![]() ,若
,若![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五张如图所示的长为![]() ,宽为
,宽为![]() 的小长方形纸片,按如图的方式不重叠地放在矩形
的小长方形纸片,按如图的方式不重叠地放在矩形![]() 中,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为
中,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为![]() ,当
,当![]() 的长度变化时,按照同样的放置方式,
的长度变化时,按照同样的放置方式,![]() 始终保持不变,则
始终保持不变,则![]() ,
,![]() 满足的关系式为( )
满足的关系式为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com