
 如图:正方形OABC的顶点O在坐标原点,点A的坐标为(12,5).
如图:正方形OABC的顶点O在坐标原点,点A的坐标为(12,5).分析 (1)作AE⊥x轴于E,根据勾股定理求出正方形OABC的边长;
(2)作BF⊥x轴于F,AG⊥BF于G,CH⊥x轴于H,证明△COH≌△OAE,根据全等三角形的性质求出OH、CH得到点C的坐标,证明△BAG≌△OAE,求出点B的坐标;
(3)分点Q在AO上和点Q在CO上两种情况,根据菱形的性质列出方程,解方程即可.
解答 解:(1)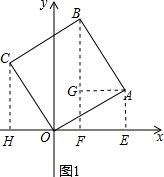 作AE⊥x轴于E,
作AE⊥x轴于E,
∵点A的坐标为(12,5),
∴OE=12,AE=5,
∴OA=$\sqrt{O{E}^{2}+A{E}^{2}}$=13,
故答案为:13;
(2)作BF⊥x轴于F,AG⊥BF于G,CH⊥x轴于H,
∵正方形OABC是正方形,
∴OC=OA,∠AOC=90°,又AE⊥x轴,
∴∠COH=∠OAE,
在△COH和△OAE中,
$\left\{\begin{array}{l}{∠COH=∠OAE}\\{∠CHO=∠OEA=90°}\\{OC=OA}\end{array}\right.$,
∴△COH≌△OAE,
∴OH=AE=5,CH=OE=12,
∴点C的坐标是(-5,12),
同理△BAG≌△OAE,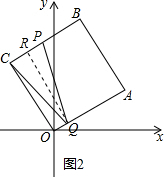
∴AG=AE=5,BG=OE=12,
∴OF=7,BF=17,
∴点B的坐标是(7,17),
故答案为:(7,17);(-5,12);
(3)①如图2,当点Q在AO上时,
设t秒后,翻折前后的两个三角形组成的四边形为菱形,则QC=QP,
作QR⊥BC于R,
则CR=$\frac{1}{2}$CP=t,OQ=13-3t,
由题意得,13-3t=t,
解得,t=$\frac{13}{4}$,
②当点Q在CO上时,
设t秒后,翻折前后的两个三角形组成的四边形为菱形,则QC=CP,
即26-3t=2t,
解得,t=$\frac{26}{5}$,
综上所述当t=$\frac{13}{4}$或$\frac{26}{5}$时,翻折前后的两个三角形组成的四边形为菱形.
点评 本题考查的是正方形的性质、翻折变换的性质以及菱形的性质和判定,掌握旋转变换的性质、菱形的判定定理是解题的关键,解答时,注意分情况讨论思想的灵活运用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 阅读时间t/h | 0≤t<2 | 2≤t<4 | 4≤t<6 | 6≤t<8 |
| 频数 | 5 | 11 | 4 |
| A. | 12.5% | B. | 40% | C. | 50% | D. | 60% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查某市中学生立定跳远的情况 | |
| B. | 调查某市市民对央视春晚的喜爱程度 | |
| C. | 调查某市市民的晨练情况 | |
| D. | 调查某班学生校服的尺寸 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com