
分析 根据化简二次根式的步骤,应用二次根式的基本性质,化简$\sqrt{4-\sqrt{6+2\sqrt{5}}}$即可.
解答 解:$\sqrt{4-\sqrt{6+2\sqrt{5}}}$
=$\sqrt{4-\sqrt{{(\sqrt{5}+1)}^{2}}}$
=$\sqrt{4-(\sqrt{5}+1)}$
=$\sqrt{3-\sqrt{5}}$
故答案为:$\sqrt{3-\sqrt{5}}$.
点评 此题主要考查了二次根式的性质和化简,要熟练掌握,化简二次根式的步骤:①把被开方数分解因式;②利用积的算术平方根的性质,把被开方数中能开得尽方的因数(或因式)都开出来;③化简后的二次根式中的被开方数中每一个因数(或因式)的指数都小于根指数2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 0.77×10-5 | B. | 0.77×10-6 | C. | 7.7×10-5 | D. | 7.7×10-6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7×10-4 | B. | 7×10-5 | C. | 0.7×10-4 | D. | 0.7×10-5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
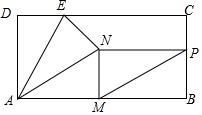 如图,已知矩形ABCD,点E是CD上的一点,AD=2$\sqrt{3}$,CD=5,将△ADE沿着AE翻折得到△AEN,若∠DAE=30°.
如图,已知矩形ABCD,点E是CD上的一点,AD=2$\sqrt{3}$,CD=5,将△ADE沿着AE翻折得到△AEN,若∠DAE=30°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com