
分析 首先统一单位:60千米/时=16.67米/秒,5分=300秒.火车与甲车是追及关系,追及问题的公式是:路程差÷速度差=追及时间.路程差是180米,追及时间是30秒,由此知道火车与甲车的速度差是:180÷30=6(米/秒).前面已求出火车的速度是16.67米/秒,由此可知甲车的速度是:16.67-6=10.67(米/秒).火车与乙车是相遇关系,路程÷相遇时间=速度和,即:180÷6=30(米/秒),则乙车的速度是:30-16.67=13.33(米/秒).当火车与乙相遇时,甲、乙两车之间的距离是:300×(16.67-10.67)=1800(米).甲、乙两车相遇还需要的时间是:1800÷(10.67+13.33)=75(秒)=1.25(分钟).
解答 解:60千米/时=16.67米/秒,5分=300秒.
①甲车的速度是:
16.67-180÷30,
=16.67-6,
=10.67(米/秒).
②当火车与乙相遇时,甲、乙两车之间的距离是:
300×(16.67-10.67),
=300×6,
=1800(米);
③乙车的速度是:
180÷6-16.67,
=30-16.67,
=13.33(米/秒);
④设甲、乙两车相遇还需要t秒相遇,
由题意:10.67t+13.33t=1800,
解得:t=75(秒),=1.25(分).
答:乙车遇到火车后再过1.25分钟与甲车相遇.
点评 这是一道难度较大的行程问题.解答此题要掌握以下关系式:①火车与甲车是追及关系,追及问题的公式是:路程差÷速度差=追及时间;②火车与乙车是相遇关系,路程÷相遇时间=速度和.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:解答题
 某笔直河道上有甲、乙两港,相距120千米,一艘轮船从甲港出发,顺流航行4小时到达乙港,休息1小时后立即返回;一艘快艇在轮船出发3小时后从乙港出发,逆流航行3小时到达甲港,并立即返回(掉头时间忽略不计).已知水流速度是5千米/时,下图表示轮船和快艇距甲港的距离y(千米)与轮船行驶时间x(小时)之间的函数关系,结合图象解答下列问题:(顺流速度=船在静水中速度+水流速度;逆流速度=船在静水中速度-水流速度)
某笔直河道上有甲、乙两港,相距120千米,一艘轮船从甲港出发,顺流航行4小时到达乙港,休息1小时后立即返回;一艘快艇在轮船出发3小时后从乙港出发,逆流航行3小时到达甲港,并立即返回(掉头时间忽略不计).已知水流速度是5千米/时,下图表示轮船和快艇距甲港的距离y(千米)与轮船行驶时间x(小时)之间的函数关系,结合图象解答下列问题:(顺流速度=船在静水中速度+水流速度;逆流速度=船在静水中速度-水流速度)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
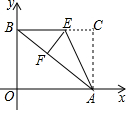 如图,已知AOBC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点B在y轴的正半轴上,点C的坐标为(8,6),在BC边上取一点E,将纸片沿AE翻折,使点C恰好落在AB边上的点F处.
如图,已知AOBC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点B在y轴的正半轴上,点C的坐标为(8,6),在BC边上取一点E,将纸片沿AE翻折,使点C恰好落在AB边上的点F处.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
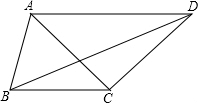 如图,在△ACD中,∠ACD=90°,AC=DC,∠ABC=75°,若AB=3$\sqrt{2}$,BC=5,则BD的长为7$\sqrt{2}$.
如图,在△ACD中,∠ACD=90°,AC=DC,∠ABC=75°,若AB=3$\sqrt{2}$,BC=5,则BD的长为7$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | -$\sqrt{3}$ | C. | -$\frac{\sqrt{6}}{2}$ | D. | -$\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com