


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源:2004年全国中考数学试题汇编《二次函数》(02)(解析版) 题型:填空题
| 抛物线 | 对称轴 | 顶点坐标 | 图象的特征 |
| y=ax2 | x=0 | (0,0) | 对称轴为y轴,顶点在原点,a>0时,开口向上,最低点是顶点;a<0时,开口向下,最高点是顶点. |
| y=a(x+1)2-1 | x= | (-1,-1) | 形状与y=ax2相同,图象可由y=ax2的图象分别向 和 平移一个单位而得. |
查看答案和解析>>
科目:初中数学 来源:2004年云南省玉溪市中考数学试卷(解析版) 题型:解答题
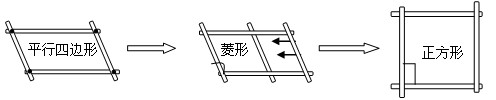

查看答案和解析>>
科目:初中数学 来源:2004年云南省玉溪市中考数学试卷(解析版) 题型:填空题
| 抛物线 | 对称轴 | 顶点坐标 | 图象的特征 |
| y=ax2 | x=0 | (0,0) | 对称轴为y轴,顶点在原点,a>0时,开口向上,最低点是顶点;a<0时,开口向下,最高点是顶点. |
| y=a(x+1)2-1 | x= | (-1,-1) | 形状与y=ax2相同,图象可由y=ax2的图象分别向 和 平移一个单位而得. |
查看答案和解析>>
科目:初中数学 来源:2004年北京市石景山区初中升学模拟考试试卷(解析版) 题型:填空题
| 图形 | 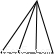 |  | 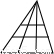 |
| 横截线条数 | 1 | 2 | |
| 三角形个数 | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com