
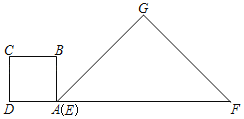
【题目】在△EFG中,∠G=90°,![]() ,正方形ABCD的边长为1,将正方形ABCD和△EFG如图放置,AD与EF在一条直线上,点A与点E重合.现将正方形ABCD沿EF方向以每秒1个单位的速度匀速运动,当点A与点F重合时停止.在这个运动过程中,正方形ABCD和△EFG重叠部分的面积S与运动时间t的函数图象大致是( )
,正方形ABCD的边长为1,将正方形ABCD和△EFG如图放置,AD与EF在一条直线上,点A与点E重合.现将正方形ABCD沿EF方向以每秒1个单位的速度匀速运动,当点A与点F重合时停止.在这个运动过程中,正方形ABCD和△EFG重叠部分的面积S与运动时间t的函数图象大致是( )
A.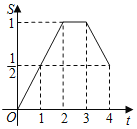 B.
B.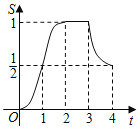
C.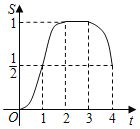 D.
D.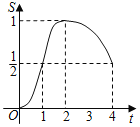
【答案】C
【解析】
分0≤t≤1、1<t≤2、2<t≤3、3<t≤4分别求出函数表达式即可求解.
解:EG=FG=![]() ,则EF=4,
,则EF=4,
①当0≤t≤1时,如图1,设AB交EG于点H,
则AE=t=AH,
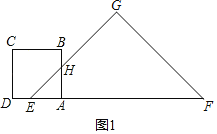
S=![]() ×AE×AH=
×AE×AH=![]() t2,函数为开口向上的抛物线,当t=1时,y=
t2,函数为开口向上的抛物线,当t=1时,y=![]() ;
;
②当1<t≤2时,如图2,设直线EG交BC于点G,交CD于点H,
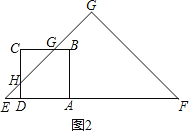
则ED=AE﹣AD=t﹣1=HD,则CH=CD﹣HD=2﹣t=CG,
S=S正方形ABCD﹣S△CGH=1﹣![]() ×CH×CG=1﹣
×CH×CG=1﹣![]() (2﹣t)2,函数为开口向下的抛物线,当t=2时,y=1;
(2﹣t)2,函数为开口向下的抛物线,当t=2时,y=1;
③当2<t≤3时,
S=S正方形ABCD=1,
④当3<t≤4时,
同理可得:S=1﹣![]() (t﹣3)2,为开口向下的抛物线;
(t﹣3)2,为开口向下的抛物线;
故选:C.


科目:初中数学 来源: 题型:
【题目】已知抛物线y1=ax2-2amx+am2+4,直线y2=kx-km+4,其中a≠0,a、k、m是常数.
(1)抛物线的顶点坐标是______,并说明上述抛物线与直线是否经过同一点(说明理由);
(2)若a<0,m=2,t≤x ≤t+2,y1的最大值为4,求t的范围;
(3)抛物线的顶点为P,直线与抛物线的另一个交点为Q,对任意的m值,若1≤k≤4,线段PQ(不包括端点)上至少存在两个横坐标为整数的点,求a的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于函数![]() (a是常数),有下列说法:
(a是常数),有下列说法:
①函数图象与坐标轴总有三个不同的交点;
②当x<1时,不是y随x的增大而增大就是y随x的增大而减小;
③若函数有最大值,则最大值必为正数,若函数有最小值,则最小值必为负数.
其中错误的说法是( )
A.①B.①②C.②③D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中抛物线y=(x+1)(x﹣3)与x轴相交于A、B两点,若在抛物线上有且只有三个不同的点C1、C2、C3,使得△ABC1、△ABC2、△ABC3的面积都等于m,则m的值是( )
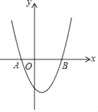
A. 6 B. 8 C. 12 D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+2交x轴于点A(-1,0),B(n,0)(点A在点B的左边),交y轴于点C.
(1)当n=2时求△ABC的面积.
(2)若抛物线的对称轴为直线x=m,当1<n<4时,求m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在同一平面内,两条平行的高速公路AB和CD之间有一条“L”型道路连通,“L”型道路中的EP=FP=20千米,∠BEP=12°,∠EPF=80°,求AB和CD之间的距离.(参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)
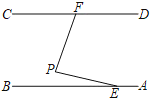
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某区2014年八年级学生的体育测试情况,随机抽取了该区若干名八年级学生的测试成绩进行了统计分析,并根据抽取的成绩等级绘制了如下的统计图表![]() :
:
成绩等级 | A | B | C | D |
人数 | 60 | 10 |
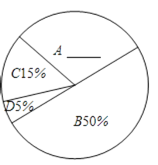
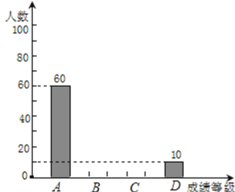
请根据以上统计图表提供的信息,解答下列问题:
(1)本次抽查的学生有______ 名,成绩为B类的学生人数为______ 名,C类成绩所在扇形的圆心角度数为______
(2)请补全条形统计图;
(3)根据抽样调查结果,请估计该区约5000名八年级学生体育测试成绩为D类的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (a≠0)的图象如图所示,则下列结论中正确的是
(a≠0)的图象如图所示,则下列结论中正确的是
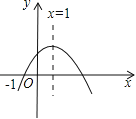
A. a>0 B. 当﹣1<x<3时,y>0
C. c<0 D. 当x≥1时,y随x的增大而增大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com