
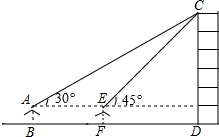
 某数学兴趣小组在学习了《锐角三角函数》以后,开展测量物体高度的实践活动,测量一建筑物CD的高度,他们站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走20m,到达点F处测得楼顶C的仰角为45°(BFD在同一直线上).已知观测员的眼睛与地面距离为1.5m(即AB=1.5m),求这栋建筑物CD的高度.(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414.结果保留整数)
某数学兴趣小组在学习了《锐角三角函数》以后,开展测量物体高度的实践活动,测量一建筑物CD的高度,他们站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走20m,到达点F处测得楼顶C的仰角为45°(BFD在同一直线上).已知观测员的眼睛与地面距离为1.5m(即AB=1.5m),求这栋建筑物CD的高度.(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414.结果保留整数) 分析 延长AE交CD于点G.设CG=xm,根据∠CEG=45°可知EG=CG=xm,在直角△ACG中,利用锐角三角函数的定义可得出x的值,进而得出结论.
解答  解:延长AE交CD于点G.设CG=xm,
解:延长AE交CD于点G.设CG=xm,
在直角△CGE中,∠CEG=45°,则EG=CG=xm.
在直角△ACG中,AG=$\frac{CG}{tan30°}$=$\sqrt{3}$xm.
∵AG-EG=AE,
∴$\sqrt{3}$x-x=20,
解得:x=10($\sqrt{3}$+1)≈27.32.
则CD=27.32+1.5=28.82≈29(m).
答:这栋建筑物CD的高度约为29m.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,熟记锐角三角函数的定义是解答此题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,小军、小英之间的距离为3m,他们在同一盏路灯下的影长均为1.8m,1.8m,已知小军、小英的身高分别为1.8m,1.5m,则路灯的高为3m.
如图,小军、小英之间的距离为3m,他们在同一盏路灯下的影长均为1.8m,1.8m,已知小军、小英的身高分别为1.8m,1.5m,则路灯的高为3m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图所示,在四边形ABCD中,E、F分别为AB、CD的中点
已知:如图所示,在四边形ABCD中,E、F分别为AB、CD的中点查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 椪柑品种 | A | B | C |
| 每辆汽车运载量(吨) | 10 | 8 | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com