
分析 (1)根据发现的规律进行计算即可;
(2)根据规律容易得出结果;
(3)根据发现的规律进行计算即可.
解答 解(1)1-$\frac{1}{1×2}$-$\frac{1}{2×3}$-$\frac{1}{3×4}$-…-$\frac{1}{20×21}$
=1-(1-$\frac{1}{21}$)
=$\frac{1}{21}$
(2)第20个等式为:$\frac{2}{39×41}=\frac{1}{39}-\frac{1}{41}$;
故答案为:$\frac{2}{39×41}=\frac{1}{39}-\frac{1}{41}$;
(3):$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{99×101}$
=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{99}$-$\frac{1}{100}$)
=$\frac{1}{2}$(1-$\frac{1}{100}$)
=$\frac{99}{200}$.
点评 本题考查了有理数的混合运算、数字的变化类;根据发现的规律进行计算是解决问题的关键.


科目:初中数学 来源: 题型:选择题
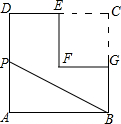 如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致为( )
如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致为( )| A. | 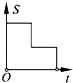 | B. | 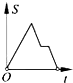 | C. | 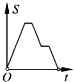 | D. | 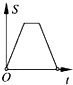 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
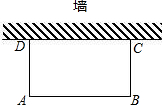 如图,某中学为中考体育加试利用一面墙(墙的长度不超过45m),用80m的铁丝网围成一个矩形体育场地.
如图,某中学为中考体育加试利用一面墙(墙的长度不超过45m),用80m的铁丝网围成一个矩形体育场地.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 候选人 | 教学能力 | 科研能力 | 组织能力 |
| 甲 | 91 | 80 | 78 |
| 乙 | 81 | 74 | 85 |
| 丙 | 79 | 83 | 90 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com