
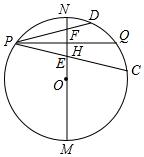
 我们知道:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧;平分弧的直径垂直平分这条弧所对的弦.你可以利用这一结论解决问题:
我们知道:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧;平分弧的直径垂直平分这条弧所对的弦.你可以利用这一结论解决问题:分析 (1)根据等腰三角形的性质,由PE=PF,PH⊥EF可判断PH平分∠FPE,然后根据圆周角定理得到$\widehat{CQ}$=$\widehat{DQ}$;
(2)连结CD、OP、OQ,OQ交CD于B,如图,先计算出PH=2$\sqrt{2}$,则可判断△OPH为等腰直角三角形得到∠OPQ=45°,再判断△OPQ为等腰直角三角形得到∠POQ=90°,然后根据垂径的推理由$\widehat{CQ}$=$\widehat{DQ}$得到OQ⊥CD,
则根据平行线的判定方法得OP∥CD;
(3)直线CD交MN于A,如图,由特殊角的三角函数值得∠α=30°,即直线MN、CD相交所成的锐角为30°,利用OB⊥CD得到∠AOB=60°,则∠POH=60°,然后在Rt△POH中利用正弦的定义计算出PH即可.
解答 (1)解:∵PE=PF,PH⊥EF,
∴PH平分∠FPE,
∴∠DPQ=∠CPQ,
∴$\widehat{CQ}$=$\widehat{DQ}$;
(2)证明:连结CD、OP、OQ,OQ交CD于B,如图,
∵OH=2$\sqrt{2}$,OP=4,
∴PH=$\sqrt{{4}^{2}-(2\sqrt{2})^{2}}$=2$\sqrt{2}$,
∴△OPH为等腰直角三角形,
∴∠OPQ=45°,
而OP=OQ,
∴△OPQ为等腰直角三角形,
∴∠POQ=90°,
∴OP⊥OQ,
∵$\widehat{CQ}$=$\widehat{DQ}$,
∴OQ⊥CD,
∴OP∥CD;
(3)解:直线CD交MN于A,如图,
∵cosα=$\frac{\sqrt{3}}{2}$,
∴∠α=30°,即直线MN、CD相交所成的锐角为30°,
而OB⊥CD,
∴∠AOB=60°,
∵OH⊥PQ,
∴∠POH=60°,
在Rt△POH中,∵sin∠POH=$\frac{PH}{OP}$,
∴PH=4sin60°=2$\sqrt{3}$,
即点P到MN的距离为2$\sqrt{3}$.
点评 本题考查了圆的综合题:熟练掌握垂径定理及其推理、圆周角定理;能够灵活应用等腰直角三角形的性质和三角函数进行几何计算.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
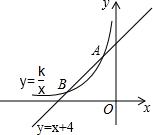 如图,直线y=x+4与双曲线y=$\frac{k}{x}$(k≠0)相交于A(-1,a)、B两点,在y轴上找一点P,当PA+PB的值最小时,点P的坐标为(0,$\frac{5}{2}$).
如图,直线y=x+4与双曲线y=$\frac{k}{x}$(k≠0)相交于A(-1,a)、B两点,在y轴上找一点P,当PA+PB的值最小时,点P的坐标为(0,$\frac{5}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
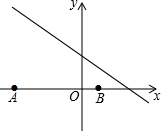 如图,已知点A(-8,0),B(2,0),点C在直线y=-$\frac{3}{4}x+4$上,则使△ABC是直角三角形的点C的个数为( )
如图,已知点A(-8,0),B(2,0),点C在直线y=-$\frac{3}{4}x+4$上,则使△ABC是直角三角形的点C的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1,正八边形外侧八个扇形(阴影部分)面积之和为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1,正八边形外侧八个扇形(阴影部分)面积之和为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{3}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com