
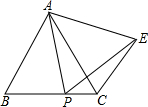
 如图,△ABC是等边三角形,P为BC上一动点(不与B、C重合),以AP为边作等边△APE,连接CE.
如图,△ABC是等边三角形,P为BC上一动点(不与B、C重合),以AP为边作等边△APE,连接CE.
|


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在梯形ABCD中,AD∥BC,∠DCB=90°,点E是边AB的中点,联结DE,延长DE交CB的延长线于点F,∠CBA=2∠F,且AC=BC.
如图,在梯形ABCD中,AD∥BC,∠DCB=90°,点E是边AB的中点,联结DE,延长DE交CB的延长线于点F,∠CBA=2∠F,且AC=BC.查看答案和解析>>
科目:初中数学 来源: 题型:
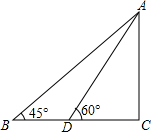 如图,在广场上用氢气球悬挂着“人文黔东南,和谐黔东南,美丽黔东南,建设黔东南”的大型宣传条幅AC.小明站在B处看条幅顶端A的仰角为45°,再往条幅方向前往20米到D处,在D处看条幅顶端A的仰角为60°,求条幅AC的高度(小明的身高不计,条幅垂直于地面)(结果精确到0.1米,参考数据
如图,在广场上用氢气球悬挂着“人文黔东南,和谐黔东南,美丽黔东南,建设黔东南”的大型宣传条幅AC.小明站在B处看条幅顶端A的仰角为45°,再往条幅方向前往20米到D处,在D处看条幅顶端A的仰角为60°,求条幅AC的高度(小明的身高不计,条幅垂直于地面)(结果精确到0.1米,参考数据| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com