
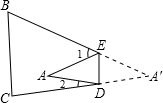
 如图所示,把纸片△A′BC沿DE折叠,点A′落在四边形BCDE内部点A处.
如图所示,把纸片△A′BC沿DE折叠,点A′落在四边形BCDE内部点A处.分析 (1)根据折叠的性质,可得出△ADE≌△A′DE,再根据全等三角形的性质即可得出答案;
(2)由折叠的性质得出,∠1+2∠AED=180°,∠2+2∠ADE=180°,从而得出∠1,∠2的度数;
(3)由折叠的性质得出,∠A=∠A′,再由三角形的内角和定理得出∠A与∠1+∠2的关系.
解答 解:(1)由折叠的性质得出△ADE≌△A′DE,∠ADE=∠A′DE,∠AED=∠A′ED,∠A=∠A′,
(2)∵∠1+2∠AED=180°,∠2+2∠ADE=180°,
∴∠1=180°-2∠AED,∠2=180°-2∠ADE,
∵∠AED=x,∠ADE=y,
∴∠1=180°-2∠AED=180°-2x,∠2=180°-2∠ADE=180°-2y,
(3)∵∠A′+∠A′DE+∠A′ED=180°,
∴∠A′DE+∠A′ED=180°-∠A′,
∵∠A=∠A′,
∴∠A′DE+∠A′ED=180°-∠A,
∵∠A′DE=∠ADE,∠A′ED=∠AED
∴∠ADE+∠AED=180°-∠A,
∵∠1+2∠AED=180°,∠2+2∠ADE=180°,
∴∠AED+∠ADE=180°-∠1-∠2,
∴∠A=∠1+∠2.
点评 本题考查了全等三角形的判定,以及三角形的内角和定理:三角形的内角和等于180度,掌握折叠的性质是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
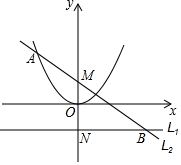 已知a>0,直线L1:y=-$\frac{1}{4a}$与y轴交于点N,点N关于原点的对称点为点M,过点M的直线L2与抛物线y=ax2在第二象限交于点A,与直线L1交于点B,且MA=MB,平移直线L2,使之与抛物线有唯一公共点,且与y轴交于点P.求证:$\frac{OM}{OP}$为一定值.
已知a>0,直线L1:y=-$\frac{1}{4a}$与y轴交于点N,点N关于原点的对称点为点M,过点M的直线L2与抛物线y=ax2在第二象限交于点A,与直线L1交于点B,且MA=MB,平移直线L2,使之与抛物线有唯一公共点,且与y轴交于点P.求证:$\frac{OM}{OP}$为一定值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
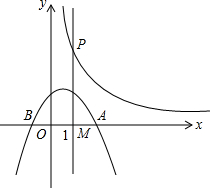 如图,抛物线L:y=-$\frac{1}{2}$(x-t)(x-t+4)(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=$\frac{k}{x}$(k>0,x>0)于点P,且OA•MP=12.
如图,抛物线L:y=-$\frac{1}{2}$(x-t)(x-t+4)(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=$\frac{k}{x}$(k>0,x>0)于点P,且OA•MP=12.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
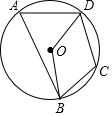 如图四边形ABCD的四个顶点在同一个圆上,这样的四边四边形叫做圆内接四边形.
如图四边形ABCD的四个顶点在同一个圆上,这样的四边四边形叫做圆内接四边形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com