
 如图所示,某数学活动小组要测量山坡上的电线杆PQ的高度,他们在A处测得信号塔顶端P的仰角是45°,信号塔底端点Q的仰角为31°,沿水平地面向前走100米到B处,测得信号塔顶端P的仰角是68°,求信号塔PQ的高度.(结果精确到0.1米,参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.48,tan31°≈0.60,sin31°≈0.52,cos31°≈0.86)
如图所示,某数学活动小组要测量山坡上的电线杆PQ的高度,他们在A处测得信号塔顶端P的仰角是45°,信号塔底端点Q的仰角为31°,沿水平地面向前走100米到B处,测得信号塔顶端P的仰角是68°,求信号塔PQ的高度.(结果精确到0.1米,参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.48,tan31°≈0.60,sin31°≈0.52,cos31°≈0.86) 分析 延长PQ交直线AB于点E,连接AQ,设PM的长为x米,先由三角函数得出方程求出PM,再由三角函数求出QM,得出PQ的长度即可.
解答 解:延长PQ交直线AB于点M,连接AQ,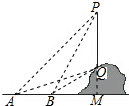 如图所示:
如图所示:
则∠PMA=90°,
设PM的长为x米,
在Rt△PAM中,∠PAM=45°,
∴AM=PM=x米,
∴BM=x-100(米),
在Rt△PBM中,∵tan∠PBM=$\frac{PM}{BM}$,
∴tan68°=$\frac{x}{x-100}$≈2.48,
解得:x≈167.57,
在Rt△QAM中,∵tan∠QAM=$\frac{QM}{AM}$,
∴QM=AM•tan∠QAM=167.57×tan31°≈167.57×0.60≈100.54(米),
∴PQ=PM-QM=167.57-100.54≈67.0(米);
答:信号塔PQ的高度约为67.0米.
点评 本题考查解直角三角形的应用、三角函数;由三角函数得出方程是解决问题的关键,注意掌握当两个直角三角形有公共边时,先求出这条公共边的长是解答此类题的一般思路.


科目:初中数学 来源: 题型:解答题
| 销售价x(元/件) | … | 110 | 115 | 120 | 125 | 130 | … |
| 销售量y(件) | … | 50 | 45 | 40 | 35 | 30 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在矩形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B→C→D作匀速运动,那么△ABP的面积y与点P运动的路程x之间的函数图象大致是( )
如图,在矩形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B→C→D作匀速运动,那么△ABP的面积y与点P运动的路程x之间的函数图象大致是( )| A. | 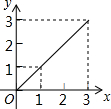 | B. | 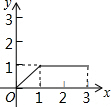 | C. | 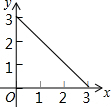 | D. | 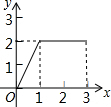 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
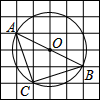 如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点.作△ABC的外接圆⊙O,则$\widehat{BC}$的长等于( )
如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点.作△ABC的外接圆⊙O,则$\widehat{BC}$的长等于( )| A. | $\frac{\sqrt{5}}{2}$π | B. | $\frac{\sqrt{5}}{4}$π | C. | $\frac{\sqrt{3}}{2}$π | D. | $\frac{\sqrt{3}}{4}$π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com