
【题目】已知二次函数y=ax2+bx+c的图象的对称轴是直线x=2,且图象过点(1,2),与一次函数y=x+m的图象交于(0,-1).
(1)求两个函数解析式;
(2)求两个函数图象的另一个交点.
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案科目:初中数学 来源: 题型:
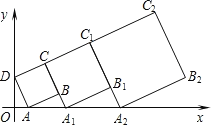
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第1个正方形A1B1C1C;延长C1B1交x轴于点A2,作第2个正方形A2B2C2C1,…,按这样的规律进行下去,第2019个正方形的面积是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
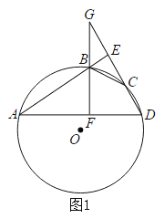
【题目】 AB,CD是![]() 的两条弦,直线AB,CD互相垂直,垂足为点E,连接AD,过点B作
的两条弦,直线AB,CD互相垂直,垂足为点E,连接AD,过点B作![]() ,垂足为点F,直线BF交直线CD于点G.
,垂足为点F,直线BF交直线CD于点G.
(1)如图1当点E在![]() 外时,连接
外时,连接![]() ,求证BE平分∠GBC;
,求证BE平分∠GBC;
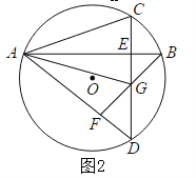
(2)如图2当点E在![]() 内时,连接AC,AG,求证:AC=AG
内时,连接AC,AG,求证:AC=AG
(3)在(2)条件下,连接BO,若BO平分![]() ,求线段EC的长.
,求线段EC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
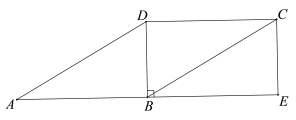
【题目】如图,在□ABCD中,∠ABD=90°,延长AB至点E,使BE=AB,连接CE.
(1)求证:四边形BECD是矩形;
(2)连接DE交BC于点F,连接AF,若CE=2,∠DAB=30°,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】M(﹣1,![]() ),N(1,
),N(1,![]() )是平面直角坐标系xOy中的两点,若平面内直线MN上方的点P满足:45°≤∠MPN≤90°,则称点P为线段MN的可视点.
)是平面直角坐标系xOy中的两点,若平面内直线MN上方的点P满足:45°≤∠MPN≤90°,则称点P为线段MN的可视点.
(1)在点![]() ,
,![]() ,
,![]() ,A4(2,2)中,线段MN的可视点为 ;
,A4(2,2)中,线段MN的可视点为 ;
(2)若点B是直线y=x![]() 上线段MN的可视点,求点B的横坐标t的取值范围;
上线段MN的可视点,求点B的横坐标t的取值范围;
(3)直线y=x+b(b≠0)与x轴交于点C,与y轴交于点D,若线段CD上存在线段MN的可视点,直接写出b的取值范围.
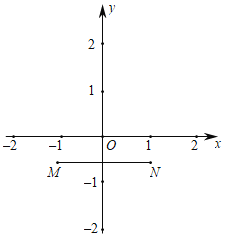
查看答案和解析>>
科目:初中数学 来源: 题型:
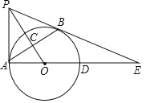
【题目】如图,PA与⊙O相切于点A,过点A作AB⊥OP,垂足为C,交⊙O于点B.连接PB,AO,并延长AO交⊙O于点D,与PB的延长线交于点E.
(1)求证:PB是⊙O的切线;
(2)若OC=3,AC=4,求PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
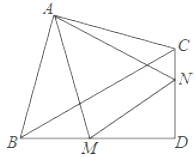
【题目】如图,在Rt△ABC和Rt△BCD中,∠BAC=∠BDC=90°,BC=4,AB=AC,∠CBD=30°,M,N分别在BD,CD上,∠MAN=45°,则△DMN的周长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
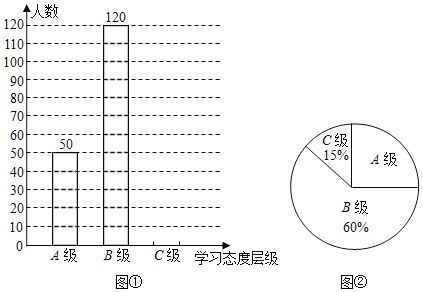
【题目】我校对八年级学生的学习态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了多少名学生;
(2)通过计算达到C级的有多少人?并补全条形图.
(3)根据抽样调查结果,请你估计我市近80000名八年级学生中大约有多少名学生学习态度达标(达标指的是学习兴趣达到A级和B级)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com