


 ,﹣
,﹣ )
) ,解它们组成的方程组得:k=
,解它们组成的方程组得:k= ,b=﹣3,
,b=﹣3, x﹣3,N点纵坐标为:﹣t,
x﹣3,N点纵坐标为:﹣t, h﹣3,∴h=2﹣
h﹣3,∴h=2﹣ t,其中
t,其中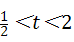 ,∴s=
,∴s= (2+t)(2﹣
(2+t)(2﹣ t)=﹣
t)=﹣ t2+
t2+ t+3,
t+3, t2+
t2+ t+3,自变量的取值围是:
t+3,自变量的取值围是: ;
; ,
, ),P2(
),P2( ).
).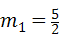 ,m2=﹣1(舍去).所以点
,m2=﹣1(舍去).所以点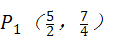 .(ⅱ)若∠PAC=90°,则PC2=PA2+AC2∴n=m2﹣m﹣2(m+1)2+n2=m2+(n+2)2+5解得:
.(ⅱ)若∠PAC=90°,则PC2=PA2+AC2∴n=m2﹣m﹣2(m+1)2+n2=m2+(n+2)2+5解得: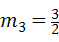 ,m4=0(舍去).所以点P2(
,m4=0(舍去).所以点P2( ,﹣
,﹣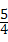 ).
).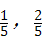 ),(
),( ,﹣
,﹣ )解析:
)解析:

科目:初中数学 来源: 题型:
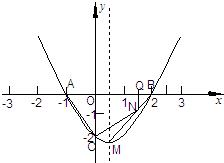
(本题12分)已知二次函数的图象经过点(0,-3),且顶点坐标为(-1,-4).
(1)求该二次函数的解析式;
(2)设该二次函数的图象与x轴的交点为A、B,与y轴的交点为C,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011年江苏省沭阳县中学中考模拟考试数学卷.doc 题型:解答题
﹣(本题12分)已知二次函数y=x2+bx+c与x轴交于A(-1,0)、B(1,0)两点.
(1)求这个二次函数的关系式;
(2)若有一半径为r的⊙P,且圆心P在抛物线上运动,当⊙P与两坐标轴都相切时,求半径r的值.
(3)半径为1的⊙P在抛物线上,当点P的纵坐标在什么范围内取值时,⊙P与y轴相离、相交?
查看答案和解析>>
科目:初中数学 来源:2012届浙江省新昌县实验中学九年级上学期期中阶段性测试数学卷 题型:解答题
(本题12分)已知二次函数的图象经过点(0,-3),且顶点坐标为(-1,-4).
(1)求该二次函数的解析式;
(2)设该二次函数的图象与x轴的交点为A、B,与y轴的交点为C,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com