
 的图象与一次函数
的图象与一次函数 的图象交于点A(1,4)和点B
的图象交于点A(1,4)和点B ,
, ).
).
 >0时,直接写出
>0时,直接写出 >
> 时自变量
时自变量 的取值范围;
的取值范围; 轴对称,求△ABC的面积.
轴对称,求△ABC的面积. 的图象上,∴
的图象上,∴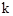 =1×4=4。
=1×4=4。
 的图象上,∴
的图象上,∴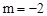 。∴点B(-2,-2)。
。∴点B(-2,-2)。  的图象上,
的图象上,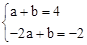 ,解得
,解得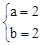 。
。 。
。  <1时,
<1时, >
> 成立
成立 轴对称,∴C(1,-4)。
轴对称,∴C(1,-4)。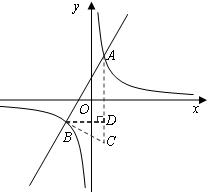
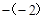 =3,底为AC=4
=3,底为AC=4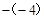 =8。
=8。 AC·BD=
AC·BD= ×8×3=12。
×8×3=12。  ,再求出B的坐标是(-2,-2),利用待定系数法求一次函数的解析式。
,再求出B的坐标是(-2,-2),利用待定系数法求一次函数的解析式。 >0时,一次函数的值小于反比例函数的值x的取值范围或0<x<1。
>0时,一次函数的值小于反比例函数的值x的取值范围或0<x<1。

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
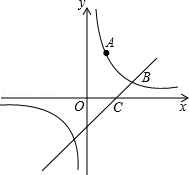
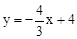 的图象与x轴、y轴分别相交于点A、B.P是射线BO上的一个动点(点P不与点B重合),过点P作PC⊥AB,垂足为C,在射线CA上截取CD=CP,连接PD.设BP=t.
的图象与x轴、y轴分别相交于点A、B.P是射线BO上的一个动点(点P不与点B重合),过点P作PC⊥AB,垂足为C,在射线CA上截取CD=CP,连接PD.设BP=t.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 打折前一次性购物总金额 | 优惠措施 |
| 不超过400元 | 售价打九折 |
| 超过400元 | 售价打八折 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com