
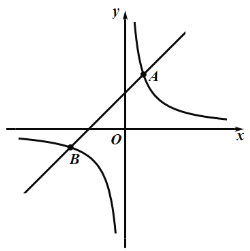
【题目】如图:反比例函数 与一次函数 的图象交于A(1,3)和B(-3,n)两点.
(1)求反比例函数与一次函数的解析式;
(2)当x取什么值时,一次函数的值大于反比例函数的值.
(3)求出△OAB的面积.
【答案】(1)![]() ,y=x+2;(2)-3<x<0或x>1;(3)4.
,y=x+2;(2)-3<x<0或x>1;(3)4.
【解析】
(1)用待定系数法,设反比例函数为![]() ,一次函数为y=
,一次函数为y=![]() x+b,把A、B坐标代入后可以解出.
x+b,把A、B坐标代入后可以解出.
(2)一次函数的值大于反比例函数,即一次函数的图像在反比例函数的上面,结合图像解出即可解出.
(3)一次函数与x轴相交于C点,![]() 即可解得.
即可解得.
解:(1)设反比例函数为![]() ,
,
把A(1,3)、B(-3,n)两点坐标代入得
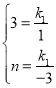
解得![]()
反比例函数解析式为![]() ;
;
再把A(1,3)、B(-3,-1)代入一次函数解析式中
得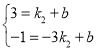
解得![]()
一次函数解析式为y=x+2.
(2)若要一次函数大于反比例函数
即一次函数的图像在反比例函数图像的上面
解得-3<x<0或x>1.
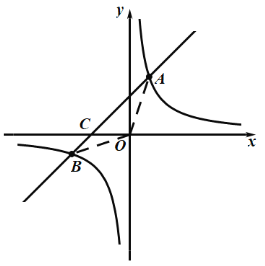
(3)设一次函数与x轴交于点C,
令y=0,得x=-2,则C点坐标为(-2,0)
![]()
=![]()
=4


科目:初中数学 来源: 题型:
【题目】草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季试销售成本为每千克18元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元.经试销发现,销售量y(kg)与销售单价x(元/kg)符合一次函数关系,如图是y与x的函数关系图象.
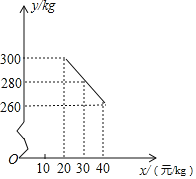
(1)求y与x的函数解析式;
(2)设该水果销售店试销草莓获得的利润为W元,求W的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解八年级学生的户外活动情况,某校随机调查了该年级部分学生双休日户外活动的时间(单位:小时),调查结果按0~1,1~2,2~3,3~4(每组含前一个边界值,不含后一个边界值)分为四个等级,并依次用A,B,C,D表示,调查人员整理数据并绘制了如图所示的不完整的统计图,请根据所给信息解答下列问题.
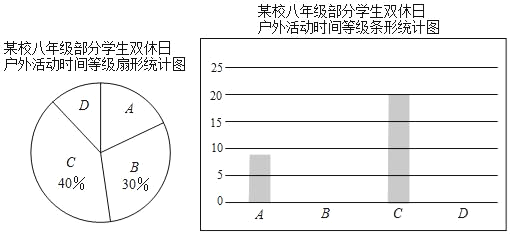
(1)求本次调查的学生人数.
(2)求等级D的学生人数,并补全条形统计图.
(3)该年级共有600名学生,估计该年级学生双休日户外活动时间不少于2小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商店以12.5元/千克的价格购进一批水果进行销售,运输过程中质量损耗5%,运输费用是0.8元/千克(运输费用按照进货质量计算),假设不计其他费用.
(1)商店要把水果售完至少定价为多少元才不会亏本?
(2)在销售过程中,商店发现每天水果的销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示,那么当销售单价定为多少时,每天获得的利润w最大?最大利润是多少?
(3)该商店决定每销售1千克水果就捐赠p元利润(p≥1)给希望工程,通过销售记录发现,销售价格大于每千克22元时,扣除捐赠后每天的利润随x增大而减小,直接写出p的取值范围.
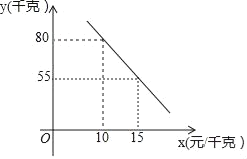
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有大小和形状相同的3个红球和2个白球,把它们充分搅匀.
(1)“从中任意抽取1个球不是红球就是白球”是 事件,“从中任意抽取1个球是黑球”是 事件;
(2)从中任意抽取1个球恰好是红球的概率是 ;
(3)学校决定在甲、乙两名同学中选取一名作为学生代表发言,制定如下规则:从盒子中任取两个球,若两球同色,则选甲;若两球异色,则选乙.你认为这个规则公平吗?请用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解九年级学生对三大球类运动的喜爱情况,从九年级学生中随机抽取部分学生进行调查问卷,通过分析整理绘制了如下两幅统计图.请根据两幅统计图中的信息回答下列问题:

(1)求参与调查的学生中,喜爱排球运动的学生人数,并补全条形图;
(2)若该中学九年级共有800名学生,请你估计该中学九年级学生中喜爱篮求运动的学生有多少名?
(3)若从喜爱足球运动的2名男生和2名女生中随机抽取2名学生,确定为该校足球运动员的重点培养对象,请用列表法或画树状图的方法求抽取的两名学生为一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=30°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围;
(3)当△ADE是等腰三角形时,求AE的长.
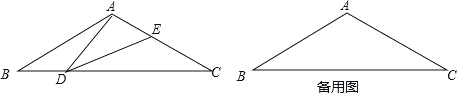
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应政府提出的“绿色发展·低碳出行”号召,某社区决定购置一批共享单车,经市场调查得知,购买3量男式单车与4辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需16000元.
(1)求男式单车和女式单车的单价;
(2)该社区要求男式单比女式单车多4辆,两种单车至少需要22辆,购置两种单车的费用不超过50000元,该社区有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com