
(2005 北京)已知:关于x的方程 有两个不相等的实数根
有两个不相等的实数根 和
和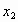 ,并且抛物线
,并且抛物线 与x轴的两个交点分别位于点(2,0)的两旁.
与x轴的两个交点分别位于点(2,0)的两旁.
(1)求实数a的取值范围;
(2)当 时,求a的值.
时,求a的值.
|
(1) 解法1 ∵关于x的方程 有两个不相等的实数根, 有两个不相等的实数根,
∴ 
解得: a<0,且a≠-2 ①设抛物线 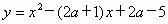 与x轴的两个交点的坐标为(α,0)、(β,0),且α>β, 与x轴的两个交点的坐标为(α,0)、(β,0),且α>β,
∴ α、β是关于x的方程 的两个不相等的实数根. 的两个不相等的实数根.
∵  , ,
∴此不等式 a为任意实数. ②由根与系数的关系得: α+β=2a+1,αβ=2a-5.∵抛物线 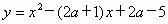 与x轴的两个交点分别位于点(2,0)的两旁, 与x轴的两个交点分别位于点(2,0)的两旁,
∴ α<2,β>2,∴ (α-2)(β-2)<0,∴ αβ-2(α+β)+4<0,∴ 2a-5-2(2a+1)+4<0,解得:  . .
由①、②、③得 a的取值范围是 . .
解法 2 同解法1,得a<0,且a≠-2①∵抛物线 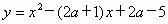 与x轴的两个交点分别位于点(2,0)两旁,且抛物线开口向上, 与x轴的两个交点分别位于点(2,0)两旁,且抛物线开口向上,
∴当 x=2时,y<0,∴ 4-2(2a+1)+2a-5<0,解得: 
由①、②得 a的取值范围是 . .
(2) 解 ∵ 和 和 是关于x的方程 是关于x的方程 的两个不相等的实数根, 的两个不相等的实数根,
∴ 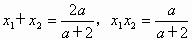 . .
∵ 
∴ a+2>0,∴  , ,
不妨设  . .
∴  , ,
∴  ,即 ,即 , ,
∴  . .
解这个方程,得:
经检验,  都是方程 都是方程 的根, 的根,
∴ a为-1为所求.此题可作高考题,难度与高考难题相近。 |
|
点评 本题主要考查二次函数不等式的有关知识,在解题时运用了分类讨论的思想,只要掌握了最基础的知识,此题便很容易解决. |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:044
(2005 北京东城)已知抛物线 .
.
(1)求证此抛物线与x轴有两个不同的交点;
(2)若m是整数,抛物线 与x轴交于整数点,求m的值;
与x轴交于整数点,求m的值;
(3)在(2)的条件下,设抛物线顶点为A,抛物线与x轴的两个交点中右侧交点为B.若M为坐标轴上一点,且MA=MB,求点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com