
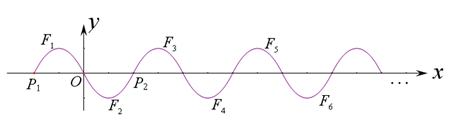
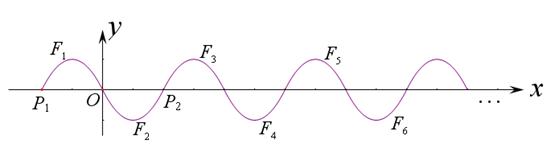
如图,抛物线 (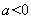 )位于
)位于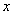 轴上方的图象记为
轴上方的图象记为 1 ,它与
1 ,它与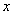 轴交于
轴交于 1 、
1 、 两点,图象
两点,图象 2与
2与 1关于原点
1关于原点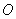 对称,
对称,  2与
2与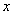 轴的另一个交点为
轴的另一个交点为 2 ,将
2 ,将 1与
1与 2同时沿
2同时沿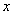 轴向右平移
轴向右平移 1
1 2的长度即可得
2的长度即可得 3与
3与 4 ;再将
4 ;再将 3与
3与 4 同时沿
4 同时沿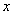 轴向右平移
轴向右平移 1
1 2的长度即可得
2的长度即可得 5与
5与 6 ; ……按这样的方式一直平移下去即可得到一系列图象
6 ; ……按这样的方式一直平移下去即可得到一系列图象 1 ,
1 , 2 ,…… ,
2 ,…… , n ,我们把这组图象称为“波浪抛物线”.
n ,我们把这组图象称为“波浪抛物线”.
⑴ 当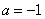 时,
时,
① 求图象 1的顶点坐标;
1的顶点坐标;
② 点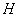 (2014 , -3) (填“在”或“不在”)该“波浪抛物线”上;若图象
(2014 , -3) (填“在”或“不在”)该“波浪抛物线”上;若图象 n 的顶点
n 的顶点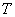 n的横坐标为201,则图象
n的横坐标为201,则图象 n 对应的解析式为______ ,其自变量
n 对应的解析式为______ ,其自变量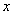 的取值范围为_______.
的取值范围为_______.
⑵ 设图象 m、
m、 m+1的顶点分别为
m+1的顶点分别为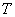 m 、
m 、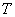 m+1 (m为正整数),
m+1 (m为正整数),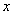 轴上一点Q的坐标为(12 ,0).试探究:当
轴上一点Q的坐标为(12 ,0).试探究:当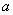 为何值时,以
为何值时,以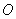 、
、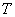 m 、
m 、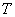 m+1、Q四点为顶点的四边形为矩形?并直接写出此时m的值.
m+1、Q四点为顶点的四边形为矩形?并直接写出此时m的值.


解析:(1)当 时,
时,
①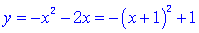 ,∴F1的顶点是(-1,1);
,∴F1的顶点是(-1,1);
②由①知:“波浪抛物线”的 值的取值范围是-1≤
值的取值范围是-1≤ ≤1,
≤1,
∴点H(2014,-3)不在“波浪抛物线”上;
由平移知:F2: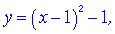 F3:
F3: ,…,
,…,
∵Fn的顶点横坐标是201,∴Fn的解析式是: ,
,
此时图象与 轴的两个交点坐标是(200,0)、(202,0),
轴的两个交点坐标是(200,0)、(202,0),
∴200≤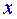 ≤202 .
≤202 .
(2)如下图,取OQ的中点O′,连接Tm Tm+1 ,
∵四边形OTmQTm+1是矩形,
∴Tm Tm+1=OQ=12, 且 Tm Tm+1 经过O′, ∴OTm+1=6,
∵F1: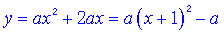
∴Tm+1的纵坐标为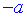 ,
,
∴(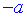 )2+12 =62 , ∴
)2+12 =62 , ∴ =±
=±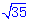 ,
,
已知 <0 , ∴
<0 , ∴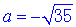 .
.
∴当 时,以以O、Tm 、Tm+1、Q四点为顶点的四边形为矩形.
时,以以O、Tm 、Tm+1、Q四点为顶点的四边形为矩形.
此时m=4.





科目:初中数学 来源: 题型:
如图,反比例函数y=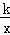 (k为常数,且k≠0)经过点A(1,3).
(k为常数,且k≠0)经过点A(1,3).
(1)求反比例函数的解析式;
(2)在x轴正半轴上有一点B,若△AOB的面积为6,求直线AB的解析式.



查看答案和解析>>
科目:初中数学 来源: 题型:
下列事件是必然事件的是( )
|
| A. | 抛掷一枚硬币四次,有两次正面朝上 |
|
| B. | 打开电视频道,正在播放《十二在线》 |
|
| C. | 射击运动员射击一次,命中十环 |
|
| D. | 方程x2﹣2x﹣1=0必有实数根 |


查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D.如果∠A=30°,AE=6cm,那么CE等于( )

|
| A. |
| B. | 2cm | C. | 3cm | D. | 4cm |


查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在x轴的正半轴上依次间隔相等的距离取点A1,A2,A3,A4,…,An分别过这些点做x轴的垂线与反比例函数y=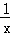 的图象相交于点P1,P2,P3,P4,…Pn作P2B1⊥A1P1,P3B2⊥A2P2,P4B3⊥A3P3,…,PnBn﹣1⊥An﹣1Pn﹣1,垂足分别为B1,B2,B3,B4,…,Bn﹣1,连接P1P2,P2P3,P3P4,…,Pn﹣1Pn,得到一组Rt△P1B1P2,Rt△P2B2P3,Rt△P3B3P4,…,Rt△Pn﹣1Bn﹣1Pn,则Rt△Pn﹣1Bn﹣1Pn的面积为
的图象相交于点P1,P2,P3,P4,…Pn作P2B1⊥A1P1,P3B2⊥A2P2,P4B3⊥A3P3,…,PnBn﹣1⊥An﹣1Pn﹣1,垂足分别为B1,B2,B3,B4,…,Bn﹣1,连接P1P2,P2P3,P3P4,…,Pn﹣1Pn,得到一组Rt△P1B1P2,Rt△P2B2P3,Rt△P3B3P4,…,Rt△Pn﹣1Bn﹣1Pn,则Rt△Pn﹣1Bn﹣1Pn的面积为 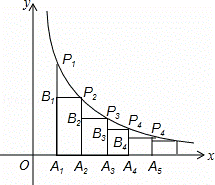


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com