
【题目】在推进郑州市城乡生活垃圾分类的行动中,某社区对居民掌握垃圾分类知识的情况进行调査.其中![]() ,
,![]() 两小区分别有1000名居民参加了测试,社区从中各随机抽取50名居民成绩进行整理得到部分信息:
两小区分别有1000名居民参加了测试,社区从中各随机抽取50名居民成绩进行整理得到部分信息:
(信息一)![]() 小区50名居民成绩的频数直方图如下(每一组含前一个边界值,不含后一个边界值).
小区50名居民成绩的频数直方图如下(每一组含前一个边界值,不含后一个边界值).
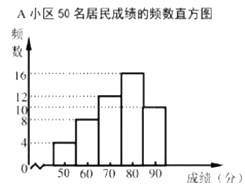
(信息二)上图中,从左往右第四组的成绩如下:
75 | 75 | 79 | 79 | 79 | 79 | 80 | 80 |
81 | 82 | 82 | 83 | 83 | 84 | 84 | 84 |
(信息三)![]() ,
,![]() 两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
小区 | 平均数 | 中位数 | 众数 | 优秀率 | 方差 |
| 75.1 | 79 | 40% | 277 | |
| 75.1 | 77 | 76 | 45% | 211 |
根据以上信息,回答下列问题:
(1)求![]() 小区50名居民成绩的中位数.
小区50名居民成绩的中位数.
(2)请估计![]() 小区1000名居民成绩能超过平均数的人数.
小区1000名居民成绩能超过平均数的人数.
(3)请尽量从多个角度(至少三个),选择合适的统计量分析![]() ,
,![]() 两小区参加测试的居民掌握垃圾分类知识的情况.
两小区参加测试的居民掌握垃圾分类知识的情况.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
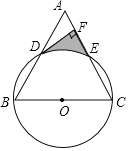
【题目】已知:如图,以等边△ABC的边BC为直径作⊙O,分别交AB,AC于点D,E,过点D作DF⊥AC交AC于点F.
(1)求证:DF是⊙O的切线;
(2)若等边△ABC的边长为8,求由![]() 、DF、EF围成的阴影部分面积.
、DF、EF围成的阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.
(1)连接GD,求证:△ADG≌△ABE;
(2)连接FC,观察并猜测∠FCN的度数,并说明理由;
(3)如图(2),将图(1)中正方形ABCD改为矩形ABCD,AB=a,BC=b(a、b为常数),E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变?若∠FCN的大小不变,请用含a、b的代数式表示tan∠FCN的值;若∠FCN的大小发生改变,请举例说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年5月26日第5届中国国际大数据产业博览会召开.某市在五届数博会上的产业签约金额的折线统计图如图.下列说法正确的是( )

A. 签约金额逐年增加
B. 与上年相比,2019年的签约金额的增长量最多
C. 签约金额的年增长速度最快的是2016年
D. 2018年的签约金额比2017年降低了22.98%
查看答案和解析>>
科目:初中数学 来源: 题型:
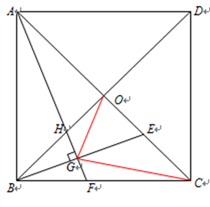
【题目】如图,在正方形ABCD中,对角线AC、BD相交于点O,E为OC上动点(与点O不重合),作AF⊥BE,垂足为G,交BC于F,交B0于H,连接OG,CC.
(1)求证:AH=BE;
(2)试探究:∠AGO的度数是否为定值?请说明理由;
(3)若OG⊥CG,BG=![]() ,求△OGC的面积.
,求△OGC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() ,对称轴交
,对称轴交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,交抛物线的对称轴于点
,交抛物线的对称轴于点![]() .
.
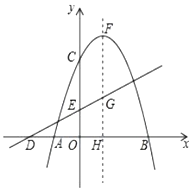
(1)求出![]() 的值.
的值.
(2)点![]() 为抛物线上一个动点,当点
为抛物线上一个动点,当点![]() 关于直线
关于直线![]() 的对称点恰好落在
的对称点恰好落在![]() 轴上时,请直接写出此时点
轴上时,请直接写出此时点![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜专业户试种植了一种紧俏蔬菜(都能卖出),其中每千克的成本![]() 在9元/千克的基础上,还有一些上浮.若浮动价(元/
在9元/千克的基础上,还有一些上浮.若浮动价(元/![]() )与需求量
)与需求量![]() (千克)成反比,比例系数为30.市场连续四天调查发现,蔬菜售价
(千克)成反比,比例系数为30.市场连续四天调查发现,蔬菜售价![]() (元/
(元/![]() )与市场需求量
)与市场需求量![]() 有如下关系:
有如下关系:
需求量 | 50 | 40 | 30 | 20 |
蔬菜售价 | 10 | 15 | 20 | 25 |
(1)直接写出每千克的成本![]() 与需求量
与需求量![]() 的关系式_________;
的关系式_________;
(2)求![]() 与
与![]() 的关系式;
的关系式;
(3)当某天的利润率达到![]() 时,求这天的需求量;
时,求这天的需求量;
(4)求需求量是多少千克时,利润达到最大值,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
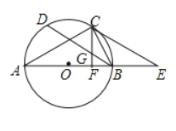
【题目】如图所示,以![]() 的边
的边![]() 为直径作
为直径作![]() ,点
,点![]() 在
在![]() 上,
上,![]() 是
是![]() 的弦,
的弦,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:![]() ;
;
(3)![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
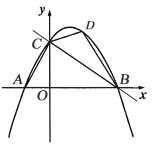
【题目】如图,在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴相交于点B、C,经过点B、C的抛物线
轴相交于点B、C,经过点B、C的抛物线![]() 与
与![]() 轴的另一个交点为A.
轴的另一个交点为A.
(1)求出抛物线表达式,并求出点A坐标;
(2)已知点D在抛物线上,且横坐标为3,求出△BCD的面积;
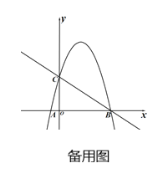
(3)点P是直线BC上方的抛物线上一动点,过点P作PQ垂直于![]() 轴,垂足为Q.是否存在点P,使得以点A、P、Q为顶点的三角形与△BOC相似?若存在,请求出点P的坐标;若不存在,请说明理由.
轴,垂足为Q.是否存在点P,使得以点A、P、Q为顶点的三角形与△BOC相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com