
【题目】如图,在直角坐标系中,四边形OABC为矩形,A(6,0),C(0,3),点M在边OA上,且M(4,0),P、Q两点同时从点M出发,点P沿x轴向右运动;点Q沿x轴先向左运动至原点O后,再向右运动到点M停止,点P随之停止运动.P、Q两点运动的速度分别为每秒1个单位、每秒2个单位.以PQ为一边向上作正方形PRLQ.设点P的运动时间为t(秒),正方形PRLQ与矩形OABC重叠部分(阴影部分)的面积为S(平方单位).
(1)用含t的代数式表示点P的坐标.
(2)分别求当t=1,t=3时,线段PQ的长.
(3)求S与t之间的函数关系式.
(4)直接写出L落在第一象限的角平分线上时t的值.

【答案】(1)P(4+t,0)(0≤t≤4);(2)当t=1时, PQ=3,当t=3时, PQ=5;(3)S=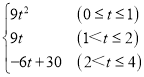 ;(4)t=
;(4)t=![]() 或
或![]() s时,L落在第一象限的角平分线上.
s时,L落在第一象限的角平分线上.
【解析】
(1)求出OP的长即可解决问题;
(2)法两种情形分别求出MQ、PM的长即可解决问题;
(3)法三种情形:①如图1中,当0≤t≤1时,重叠部分是正方形PQLR;②如图2中,当1<t≤2时,重叠部分是四边形PQDE;③如图3中,当2<t≤4时,重叠部分是四边形ABDQ,分别求解即可;
(4)根据OQ=PQ,构建方程即可解决问题.
解:(1)如图1中,∵M(4,0),
∴OM=4.PM=t,
∴OP=4+t,
∴P(4+t,0)(0≤t≤4).
(2)当t=1时,MQ=2,MP=1,
∴PQ=3.
当t=3时,MQ=2,PM=3,
∴PQ=2+3=5.
(3)①如图1中,当0≤t≤1时,重叠部分是正方形PQLR,S=PQ2=9t2

②如图2中,当1<t≤2时,重叠部分是四边形PQDE,S=PQDQ=9t.
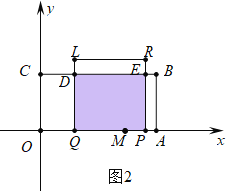
③如图3中,当2<t≤4时,重叠部分是四边形ABDQ,S=AQAB=3[6-2(t-2)]=-6t+30.
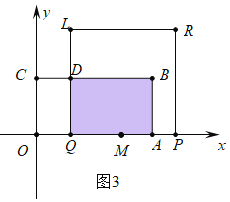
综上所述,S=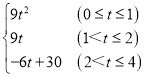 .
.
(4)L落在第一象限的角平分线上时,OQ=LQ=PQ,
∴4-2t=3t或2(t-2)=t+4-2(t-2),
解得t=![]() 或
或![]() .
.
∴t=![]() 或
或![]() s时,L落在第一象限的角平分线上.
s时,L落在第一象限的角平分线上.


科目:初中数学 来源: 题型:
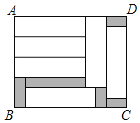
【题目】如图,在长方形ABCD中,放入6个形状和大小都相同的小长方形后,还有一部分空余(阴影部分),已知小长方形的长为a,宽为b,且a>b.
(1)用含a、b的代数式表示长方形ABCD的长AD和宽AB.
(2)用含a、b的代数式表示阴影部分的面积(列式表示即可,不要求化简).
(3)若a=7cm,b=2cm,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设抛物线![]() 与x轴的交点分别为A、B(点A在点B的左侧),顶点为C.若a、b、c满足
与x轴的交点分别为A、B(点A在点B的左侧),顶点为C.若a、b、c满足![]() ,则称该抛物线为“正定抛物线”;若a、b、c满足
,则称该抛物线为“正定抛物线”;若a、b、c满足![]() ,则称该抛物线为“负定抛物线”.特别地,若某抛物线既是“正定抛物线”又是“负定抛物线”,则称该抛物线为“对称抛物线”.
,则称该抛物线为“负定抛物线”.特别地,若某抛物线既是“正定抛物线”又是“负定抛物线”,则称该抛物线为“对称抛物线”.
(1)“正定抛物线”必经过x轴上的定点______;“负定抛物线”必经过x轴上的定点______.
(2)若抛物线![]() 是“对称抛物线”,且△ABC是等边三角形,求此抛物线对应的函数表达式.
是“对称抛物线”,且△ABC是等边三角形,求此抛物线对应的函数表达式.
(3)若抛物线![]() 是“正定抛物线”,设此抛物线交y轴于点D,△BCD的面积为S,求S与b之间的函数关系式.
是“正定抛物线”,设此抛物线交y轴于点D,△BCD的面积为S,求S与b之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 , ![]() 中,
中, ![]() ,线段
,线段![]() 在射线
在射线![]() 上,且
上,且![]() ,线段
,线段![]() 沿射线
沿射线![]() 运动,开始时,点
运动,开始时,点![]() 与点
与点![]() 重合,点
重合,点![]() 到达点
到达点![]() 时运动停止,过点
时运动停止,过点![]() 作
作![]() ,与射线
,与射线![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 的垂线,与射线
的垂线,与射线![]() 相交于点
相交于点![]() .设
.设![]() ,四边形
,四边形![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() 关于
关于![]() 的函数图象如图所示(其中
的函数图象如图所示(其中![]() 时,函数的解析式不同)
时,函数的解析式不同)
(1)填空: ![]() 的长是 ;
的长是 ;
(2)求![]() 关于
关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
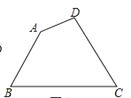
【题目】如图,现有一块四边形的木板余料ABCD,经测量AB=25cm,BC=54cm,CD=30cm,且tanB=tanC=![]() ,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,则该矩形的面积为____________.
,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,则该矩形的面积为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,矩形ABCD中,点E在DC上且DE:EC=2:3,连接BE交对角线AC于点O.延长AD交BE的延长线于点F,则△AOF与△BOC的面积之比为( )
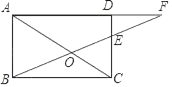
A. 9:4B. 3:2C. 25:9D. 16:9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某居民小区的一块长为b米,宽为2a米的长方形空地,为了美化环境,准备在这个长方形的四个顶点处各修建一个半径为a米的扇形花台,然后在花台内种花,其余部分种草.如果建造花台及种花费用每平方米需要资金100元,种草每平方米需要资金50元,那么美化这块空地共需资金多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若以一条线段为对角线作正方形,则称该正方形为这条线段的“对角线正方形”.例如,图①中正方形ABCD即为线段BD的“对角线正方形”.如图②,在△ABC中,∠ABC=90°,AB=3cm,BC=4cm,点P从点C出发,沿折线CA﹣AB以5cm/s的速度运动,当点P与点B不重合时,作线段PB的“对角线正方形”,设点P的运动时间为t(s),线段PB的“对角线正方形”的面积为S(cm2).
(1)如图③,借助虚线的小正方形网格,画出线段AB的“对角线正方形”.
(2)当线段PB的“对角线正方形”有两边同时落在△ABC的边上时,求t的值.
(3)当点P沿折线CA﹣AB运动时,求S与t之间的函数关系式.
(4)在整个运动过程中,当线段PB的“对角线正方形”至少有一个顶点落在∠A的平分线上时,直接写出t的值.



查看答案和解析>>
科目:初中数学 来源: 题型:
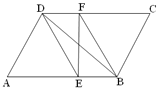
【题目】已知:如图,在□ABCD中,DE、BF分别是∠ADC和∠ABC的角平分线,交AB、CD于点E、F,连接BD、EF.
(1)求证:BD、EF互相平分;
(2)若∠A=600,AE=2EB,AD=4,求四边形DEBF的周长和面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com