
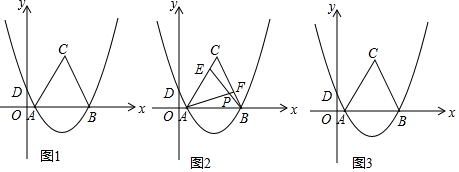
分析 (1)将点A(1,0),B(7,0)代入抛物线的解析式得到关于a、b方程组,解关于a、b的方程组求得a、b的值即可;
(2)过点C作CK⊥x轴,垂足为K.依据等边三角形的性质可求得CK=3$\sqrt{3}$,然后依据三角形的面积公式结合已知条件可求得S△ABM的面积,设M(a,$\frac{1}{4}$a2-2a+$\frac{7}{4}$),然后依据三角形的面积公式可得到关于a的方程,从而可得到点M的坐标;
(3)①首先证明△BEC≌△AFB,依据全等三角形的性质可知:AF=BE,∠CBE=∠BAF,然后通过等量代换可得到∠FAB+∠ABP=∠ABP+∠CBE=∠ABC=60°,最后依据三角形的内角和定理可求得∠APB;
②当AE≠BF时,由①可知点P在以AB为直径的圆上,过点M作ME⊥AB,垂足为E.先求得⊙M的半径,然后依据弧长公式可求得点P运动的路径;当AE=BF时,点P在AB的垂直平分线上时,过点C作CK⊥AB,则点P运动的路径=CK的长.
解答 解:(1)将点A(1,0),B(7,0)代入抛物线的解析式得:$\left\{\begin{array}{l}{49a+7b+\frac{7}{4}=0}\\{a+b+\frac{7}{4}=0}\end{array}\right.$,
解得:a=$\frac{1}{4}$,b=-2.
∴抛物线的解析式为y=$\frac{1}{4}$x2-2x+$\frac{7}{4}$.
(2)存在点M,使得S△ABM=$\frac{4\sqrt{3}}{9}$S△ABC.
理由:如图所示:过点C作CK⊥x轴,垂足为K.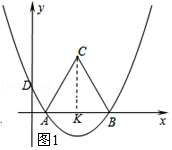
∵△ABC为等边三角形,
∴AB=BC=AC=6,∠ACB=60°.
∵CK⊥AB,
∴KA=BK=3,∠ACK=30°.
∴CK=3$\sqrt{3}$.
∴S△ABC=$\frac{1}{2}$AB•CK=$\frac{1}{2}$×6×3=9$\sqrt{3}$.
∴S△ABM=$\frac{4\sqrt{3}}{9}$×9$\sqrt{3}$=12.
设M(a,$\frac{1}{4}$a2-2a+$\frac{7}{4}$).
∴$\frac{1}{2}$AB•|y|=12,即$\frac{1}{2}$×6×($\frac{1}{4}$a2-2a+$\frac{7}{4}$)=12,
解得:a1=9,a2=-1.
∴点M的坐标为(9,4)或(-1,4).
(3)①结论:AF=BE,∠APB=120°.
∵△ABC为等边三角形,
∴BC=AB,∠C=∠ABF.
∵在△BEC和△AFB中$\left\{\begin{array}{l}{BC=AB}\\{∠C=∠ABF}\\{CE=BF}\end{array}\right.$,
∴△BEC≌△AFB.
∴AF=BE,∠CBE=∠BAF.
∴∠FAB+∠ABP=∠ABP+∠CBE=∠ABC=60°.
∴∠APB=180°-60°=120°.
②当AE≠BF时,由①可知点P在以M为圆心,在以AB为弦的圆上,过点M作MK⊥AB,垂足为k.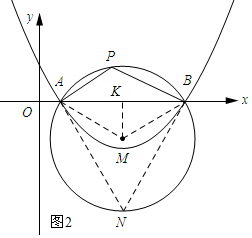
∵∠APB=120°,
∴∠N=60°.
∴∠AMB=120°.
又∵MK⊥AB,垂足为K,
∴AK=BK=3,∠AMK=60°.
∴AK=2$\sqrt{3}$.
∴点P运动的路径=$\frac{120•π×2\sqrt{3}}{180}$=$\frac{4\sqrt{3}π}{3}$.
当AE=BF时,点P在AB的垂直平分线上时,如图所示:过点C作CK⊥AB,则点P运动的路径=CK的长.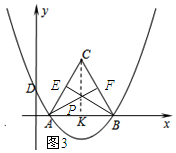
∵AC=6,∠CAK=60°,
∴KC=3$\sqrt{3}$.
∴点P运动的路径为3$\sqrt{3}$.
综上所述,点P运动的路径为3$\sqrt{3}$或$\frac{4\sqrt{3}π}{3}$.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式、等边三角形的性质、全等三角形的性质和判定、扇形的弧长公式,判断出点P运动的轨迹生成的图形的形状是解题的关键.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:解答题
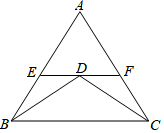 填空:把下面的推理过程补充完整,并在括号内注明理由.
填空:把下面的推理过程补充完整,并在括号内注明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 301 | B. | 302 | C. | 303 | D. | 304 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
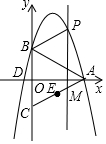 如图,已知直角坐标系中,A、B、D三点的坐标分别为A(8,0),B(0,4),D(-1,0),点C与点B关于x轴对称,连接AB、AC.
如图,已知直角坐标系中,A、B、D三点的坐标分别为A(8,0),B(0,4),D(-1,0),点C与点B关于x轴对称,连接AB、AC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在标准大气压下,水加热到100°时沸腾 | |
| B. | 小明购买1张彩票,中奖 | |
| C. | 在一个装有红球和黄球的袋中,摸出蓝球 | |
| D. | 一名运动员的速度为30米/秒 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com