
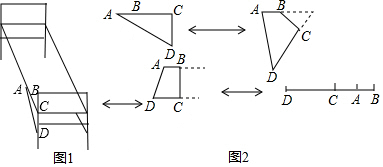
科目:初中数学 来源: 题型:选择题
| A. | 若a>b,则c-a<c-b | B. | 若c-a<c-b,则a>b | C. | 若a<b,则ac2<bc2 | D. | 若ac2<bc2,则a<b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
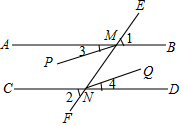 如图,直线EF分别交AB,CD于M,N,且∠1=∠2,∠3=∠4
如图,直线EF分别交AB,CD于M,N,且∠1=∠2,∠3=∠4查看答案和解析>>
科目:初中数学 来源: 题型:解答题
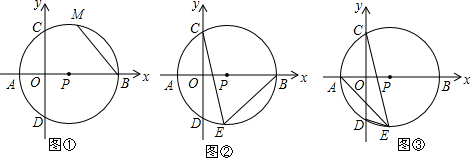
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
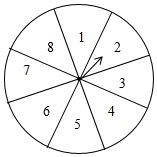 如图,一个均匀的转盘被平均分成8等份,分别标有“1,2,3,4,5,6,7,8”这8个数字,转动转盘,当转盘停止后,指针指向的数字即为转出的数字.游戏规则如下:甲、乙两个人参与游戏,甲转动转盘,乙猜数,若猜的数与转盘转出的数相符,则乙获胜;若结果不相符,则甲获胜.(若指针恰好指在分割线上,那么重转一次).
如图,一个均匀的转盘被平均分成8等份,分别标有“1,2,3,4,5,6,7,8”这8个数字,转动转盘,当转盘停止后,指针指向的数字即为转出的数字.游戏规则如下:甲、乙两个人参与游戏,甲转动转盘,乙猜数,若猜的数与转盘转出的数相符,则乙获胜;若结果不相符,则甲获胜.(若指针恰好指在分割线上,那么重转一次).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
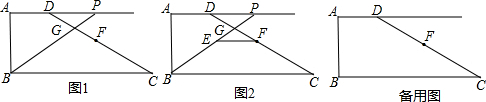
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com