练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，一个牧童在小河南4km的A处牧马，此处在也正位于他的小屋B的西12km北5km处，他想把他的马牵到小河边去饮水，然后回家，他要完成这件事情所走的最短路程是多少？
    考点：轴对称-最短路线问题
    专题：
    分析：作出A点关于MN的对称点A′，连接A′B交MN于点P，则A′B就是最短路线；然后构建直角三角形A′BD，利用勾股定理即可求得最短路程．
    解答：解：如图，作出A点关于MN的对称点A′，连接A′B交MN于点P，
    则A′B就是最短路线．
    在Rt△A′DB中，由勾股定理求得
    A′B=
    		A′D2+DB2
    =
    		(5+4+4)2+122
    =
    		313
    km．
    答：他要完成这件事情所走的最短路程是
    		313
    km．
    点评：本题考查的是勾股定理在实际生活中的运用，需要同学们联系实际，熟练掌握．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，A，B，C三点在同一直线上，△ADC，△BEC是等边三角形，连接AE，BD．求证：
    （1）EB∥CD；
    （2）AE=DB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    函数y=
    		x-4
    的自变量x的取值范围是（　　）
    A、x≠4B、x＞4
    C、x≥4D、x≤4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    先化简再求值：
    5-x
    x-3
    ÷（x+3-
    16
    x-3
    ），其中x=2sin45°-5tan45°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

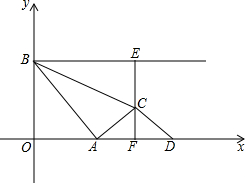    如图，点A是x轴正半轴上的动点，点B的坐标为（0，4），将线段AB的中点绕点A按顺时针方向旋转90°得点C，过点C作x轴的垂线，垂足为F，过点B作y轴的垂线与直线CF相交于点E，点D是点A关于直线CF的对称点，连接AC、BC、CD，设点A的横坐标为t．
    （1）线段AB与AC的位置关系是
     
    ；数量关系是
     
    ．
    （2）当t=2时，求CF的长；
    （3）当t为何值时，点C落在线段BD上？求出此时点C的坐标；
    （4）设△BCE的面积为S，求S与t之间的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

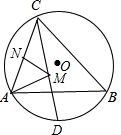    如图，△ABC内接于半径为2的⊙O，∠ABC=45°，∠ACB=60°，点D为
    AB
    的中点，点M、N分别是线段CD、AC上的动点，求MA+MN的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    分别计算图中阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

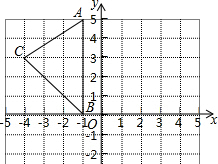    在平面直角坐标系xOy中，A（-1，5），B（-1，0），C（-4，3）．
    ①在图中作出△ABC关于y轴的对称图形△A1B1C1．
    ②求出△ABC的面积．
    ③写出点A1，B1，C1的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如表是某班同学兴趣小组的10名学生的左眼视力的统计表，那么这10名学生的左眼视力的众数是
     
    ，中位数是
     
    ，极差是
     
    ．
    左眼视力4.95.05.15.25.35.45.5
    学生人数1112131

    查看答案和解析>>

    同步练习册答案