
【题目】如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF. 
(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
【答案】
(1)证明:∵将线段CD绕点C按顺时针方向旋转90°后得CE,
∴CD=CE,∠DCE=90°,
∵∠ACB=90°,
∴∠BCD=90°﹣∠ACD=∠FCE,
在△BCD和△FCE中,
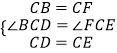 ,
,
∴△BCD≌△FCE(SAS)
(2)解:由(1)可知△BCD≌△FCE,
∴∠BDC=∠E,∠BCD=∠FCE,
∴∠DCE=∠DCA+∠FCE=∠DCA+∠BCD=∠ACB=90°,
∵EF∥CD,
∴∠E=180°﹣∠DCE=90°,
∴∠BDC=90°
【解析】(1)由旋转的性质可得:CD=CE,再根据同角的余角相等可证明∠BCD=∠FCE,再根据全等三角形的判定方法即可证明△BCD≌△FCE;(2)由(1)可知:△BCD≌△FCE,所以∠BDC=∠E,易求∠E=90°,进而可求出∠BDC的度数.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列语句中,正确的有( )
(1)相等的圆心角所对的弧相等;
(2)平分弦的直径垂直于弦;
(3)长度相等的两条弧是等弧
(4) 圆是轴对称图形,任何一条直径都是对称轴
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家为支持大学生创业,提供小额无息贷款,学生王芳享受政策无息贷款36000元用来代理品牌服装的销售.已知该品牌服装进价每件40元,日销售y(件)与销售价x(元/件)之间的关系如图所示(实线),每天付员工的工资每人每天82元,每天应支付其它费用106元.
(1)求日销售y(件)与销售价x (元/件)之间的函数关系式;
(2)若暂不考虑还贷,当某天的销售价为48元/件时,收支恰好平衡(收入=支出),求该店员工人数;
(3)若该店只有2名员工,则该店至少需要多少天才能还清贷款,此时,每件服装的价格应定为多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD. 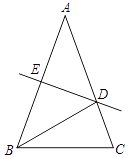
(1)若∠ABC=∠C,∠A=40°,求∠DBC的度数;
(2)若AB=AC,且△BCD的周长为18cm,△ABC的周长为30cm,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com