
【题目】如图,直线l1的函数解析式为y=﹣2x+4,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C.
(1)求直线l2的函数解析式;
(2)求△ADC的面积;
(3)在直线l2上是否存在点P,使得△ADP面积是△ADC面积的2倍?如果存在,请求出P坐标;如果不存在,请说明理由.

【答案】(1)直线l2的函数解析式为y=x﹣5(2)3(3)在直线l2上存在点P(1,﹣4)或(9,4),使得△ADP面积是△ADC面积的2倍.
【解析】试题分析:(1)根据A、B的坐标,设直线l2的函数解析式为y=kx+b,利用待定系数发求出函数l2的解析式;
(2)由函数的解析式联立方程组,求解方程组,得到C点坐标,令y=-2x+4=0,求出D点坐标,然后求解三角形的面积;
(3)假设存在,根据两三角形面积间的关系|yP|=2|yC|,=4,再根据一次函数图像上点的坐标特征即可求出P点的坐标.
试题解析:(1)设直线l2的函数解析式为y=kx+b,
将A(5,0)、B(4,﹣1)代入y=kx+b,
![]() ,解得:
,解得: ![]() ,
,
∴直线l2的函数解析式为y=x﹣5.
(2)联立两直线解析式成方程组,
![]() ,解得:
,解得: ![]() ,
,
∴点C的坐标为(3,﹣2).
当y=﹣2x+4=0时,x=2,
∴点D的坐标为(2,0).
∴S△ADC=![]() AD|yC|=
AD|yC|=![]() ×(5﹣2)×2=3.
×(5﹣2)×2=3.
(3)假设存在.
∵△ADP面积是△ADC面积的2倍,
∴|yP|=2|yC|=4,
当y=x﹣5=﹣4时,x=1,
此时点P的坐标为(1,﹣4);
当y=x﹣5=4时,x=9,
此时点P的坐标为(9,4).
综上所述:在直线l2上存在点P(1,﹣4)或(9,4),使得△ADP面积是△ADC面积的2倍.


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
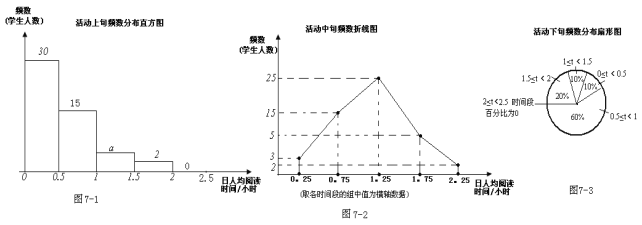
【题目】以下统计图描述了九年级(1)班学生在为期一个月的读书月活动中,三个阶段(上旬、中旬、下旬)日人均阅读时间的情况:
(1)从以上统计图可知,九年级(1)班共有学生 人;
(2)图7-1中a的值是 ;
(3)从图7-1、7-2中判断,在这次读书月活动中,该班学生每日阅读时间 (填“普遍增加了”或“普遍减少了”);
(4)通过这次读书月活动,如果该班学生初步形成了良好的每日阅读习惯,参照以上统计图的变化趋势,至读书月活动结束时,该班学生日人均阅读时间在0.5~1小时的人数比活动开展初期增加了 人。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=2x2+4x﹣5,设自变量的值分别为x1、x2、x3 , 且﹣1<x1<x2<x3 , 则对应的函数值y1、y2、y3的大小关系为( )
A.y1>y2>y3
B.y1<y2<y3
C.y2<y3<y1
D.y2>y3>y1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“五·一”节期间,某商场举行抽奖促销活动.抽奖办法是:在一个不透明的袋子中装有四个标号分别为1,2,3,4的小球,它们的形状、大小、质地等完全相同.抽奖者第一次摸出一个小球,不放回,第二次再摸出一个小球,若两次摸出的小球中有一个小球标号为“1”,则获奖.
(1)请你用树形图或列表法表示出抽奖所有可能出现的结果;
(2)求抽奖人员获奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com