

分析 (1)证明△BAM≌△CBF,根据全等三角形的性质证明;
(2)作EH⊥CD于H,根据全等三角形的性质求出FH,根据梯形的面积公式计算;
(3)根据勾股定理求出AM,根据相似三角形的性质列出比例式,计算即可.
解答 (1)证明:∵EG⊥AM,
∴∠BAM+∠ABG=90°,又∠CBF+∠ABG=90°,
∴∠BAM=∠CBF,
在△BAM和△CBF中,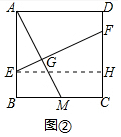
$\left\{\begin{array}{l}{∠BAM=∠CBF}\\{AB=BC}\\{∠ABM=∠BCF}\end{array}\right.$,
∴△BAM≌△CBF,
∴BM=CF;
(2)解:作EH⊥CD于H,
由(1)得,△BAM≌△HEF,
∴HF=BM=2,
∴DF=4-2-x=2-x,
∴y=$\frac{1}{2}$×(4-x+2-x)×4=12-4x(0≤≤x2);
(3)当DF=1时,BE=2-x=1,
则AE=4-1=3,
由勾股定理得,AM=$\sqrt{A{B}^{2}+B{M}^{2}}$=2$\sqrt{5}$,
∵∠AGE=∠B=90°,∠EAG=∠MAB,
∴△EAG∽△MAB,
∴$\frac{AG}{AB}$=$\frac{AE}{AM}$,即$\frac{AG}{4}$=$\frac{3}{2\sqrt{5}}$,
解得,AG=$\frac{6\sqrt{5}}{5}$,即点A到EF的距离为$\frac{6\sqrt{5}}{5}$.
点评 本题考查的是正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质,掌握全等三角形的判定定理和性质定理、相似三角形的判定定理和性质定理是解题的关键.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 行驶路程x(千米) | … | 100 | 150 | … |
| 油箱内剩余油量y(升) | … | 52 | 48 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
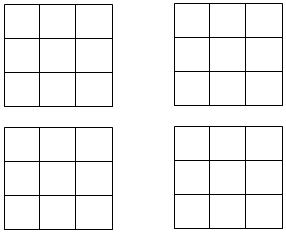 在如图所示的3×3的方格中,画出4个面积不小于1且小于9的不同的正方形,而且所画正方形的顶点都在方格的顶点上并直接写出所画正方形的面积.
在如图所示的3×3的方格中,画出4个面积不小于1且小于9的不同的正方形,而且所画正方形的顶点都在方格的顶点上并直接写出所画正方形的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
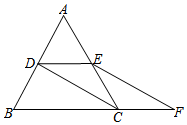 如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=$\frac{1}{2}$BC,连结CD和EF.
如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=$\frac{1}{2}$BC,连结CD和EF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
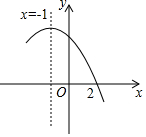 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=-1是对称轴,下列结论:①$\frac{a}{c}$<0;②a-b+c=-9a;③若(-3,y1),($\frac{3}{2}$,y2)是抛物线上两点,则y1>y2;④将抛物线沿x轴向右平移一个单位后得到的新抛物线的表达式为y=a(x2-9).其中正确的是( )
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=-1是对称轴,下列结论:①$\frac{a}{c}$<0;②a-b+c=-9a;③若(-3,y1),($\frac{3}{2}$,y2)是抛物线上两点,则y1>y2;④将抛物线沿x轴向右平移一个单位后得到的新抛物线的表达式为y=a(x2-9).其中正确的是( )| A. | ①②③ | B. | ①③④ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com