
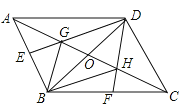
【题目】如图,已知G、H是△ABC的边AC的三等分点,GE∥BH,交AB于点E,HF∥BG交BC于点F,延长EG、FH交于点D,连接AD、DC,设AC和BD交于点O,求证:四边形ABCD是平行四边形.
科目:初中数学 来源: 题型:
【题目】阅读理解:
我们已经学习的直角三角形知识包括:勾股定理,30°、45°特殊角的直角三角形的边之间的关系等,在解决初中数学问题上起到重要作用,锐角三角函数是另一个研究直角三角形中边角间关系的知识,通过锐角三角函数也可以帮助解决数学问题.
阅读下列材料,完成习题:
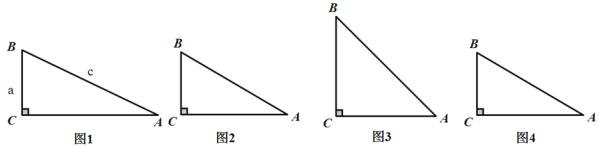
如图1,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的正弦(sine),记作sinA,即sinA=![]()
例如:a=3,c=7,则sinA=![]()
问题:在Rt△ABC中,∠C=90°
(1)如图2,BC=5,AB=8,求sinA的值.
(2)如图3,当∠A=45°时,求sinB的值.
(3)AC=2![]() ,sinB=
,sinB=![]() ,求BC的长度.
,求BC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在圣诞节来临之际,某儿童商场用2800元购进了一批玩具,上市后很快售完,商场又用7200元购进第二批这种玩具,所购数量是第一批购进数量的2倍,但每个玩具进价多了4元.
(1)该商场两次共购进这批玩具多少个?
(2)如果这两批玩具每个的售价相同,且全部售完后总利润率不低于20%,那么每个玩具的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG//CF;⑤S△FGC=3.6.其中正确结论是 . 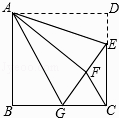
查看答案和解析>>
科目:初中数学 来源: 题型:
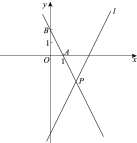
【题目】如图,在平面直角坐标系xOy中,直线![]() 的表达式为
的表达式为![]() ,点A,B的坐标分别为
,点A,B的坐标分别为
(1,0),(0,2),直线AB与直线![]() 相交于点P.
相交于点P.
(1)求直线AB的表达式;
(2)求点P的坐标;
(3)若直线![]() 上存在一点C,使得△APC的面积是△APO的面积的2倍,直接写出点C的坐标.
上存在一点C,使得△APC的面积是△APO的面积的2倍,直接写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列四个命题:
①如果某圆锥的侧面展开图是半圆,则其轴截面一定是等边三角形;
②若点A在直线y=2x﹣3上,且点A到两坐标轴的距离相等,则点A在第一或第四象限;
③半径为5的圆中,弦AB=8,则圆周上到直线AB的距离为2的点共有四个;
④若A(a,m)、B(a﹣1,n)(a>0)在反比例函y= ![]() 的图象上,则m<n.
的图象上,则m<n.
其中,正确命题的个数是( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com