
��֪������������ ��nΪ����������0<a1<a2<��<an����x��Ľ���ΪAn-1��bn-1,0����An(bn��0)����n=1ʱ����1��������
��nΪ����������0<a1<a2<��<an����x��Ľ���ΪAn-1��bn-1,0����An(bn��0)����n=1ʱ����1��������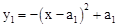 ��x��Ľ���ΪA0��0��0����A1��b1��0���������������ƣ�
��x��Ľ���ΪA0��0��0����A1��b1��0���������������ƣ�
��1����a1,b1��ֵ��������y2�Ľ���ʽ��
��2��������y3�Ķ�������Ϊ�� �� ����
�������Ƶ�n��������yn�Ķ�������Ϊ�� �� ��;
���������ߵĶ�����������ĺ�����ϵ�� ��
��3��̽�����н��ۣ�
������An-1An��ʾ��n�������߱�x��صõ��߶γ���ֱ��д��A0A1��ֵ�������An-1An��
���Ƿ���ھ�����A��2��0����ֱ�ߺ����������߶��ཻ���ұ�ÿһ�������߽صõ��߶εij��ȶ���ȣ������ڣ�ֱ��д��ֱ�ߵı���ʽ���������ڣ���˵�����ɣ�
�⣺��1����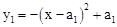 ��x�ύ�ڵ�A0��0��0������Da12+ a1=0����a1=0��1��
��x�ύ�ڵ�A0��0��0������Da12+ a1=0����a1=0��1��
����֪��֪a1>0����a1=1��
��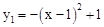 ��
��
��y1=0����ã�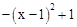 =0����x1=0��x2=2��
=0����x1=0��x2=2��
��y1��x�ύ��A0��0��0����A1��2��0������b1=2��
�֡�������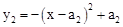 ��x�ύ�ڵ�A1��2��0����
��x�ύ�ڵ�A1��2��0����
��D(2�Da2)2+ a2=0����a2=1��4����a2> a1����a2=1����ȥ����
��ȡa2=4��������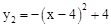 ��
��
��2����9��9���� ��n2��n2����y=x��
��3���١�A0��0��0����A1��2��0������A0 A1=2��
�֡�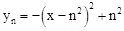 ��
��
��yn=0����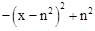 ����ã�x1=n2+n��x2=n2��n��
����ã�x1=n2+n��x2=n2��n��
��A n��1(n2��n��0)��A n(n2+n��0)����A n��1 A n=( n2+n)��( n2��n)=2 n��
�ڴ��ڡ���ƽ����ֱ��y=x�ҹ�A1��2��0����ֱ�ߣ������ʽΪy=x��2��
��������
�����������1����A0�������y1�Ľ���ʽ�����a1��ֵ��a1��ֵ֪����y1�Ľ���ʽҲ��ȷ���ˣ���֪�����߾Ϳ����b1��ֵ���ְѣ�b1��0������y2�������a2 ������y2�Ľ���ʽ��
��2����ͬ���ķ��������a3 ��a4
��a5 �����ɴ˵õ�����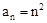 ��
��
��������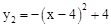 ��y2=0����ã�
��y2=0����ã�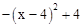 ����x1=2��x2=6��
����x1=2��x2=6��
��y2��x�ύ�ڵ�A1��2��0����A2��6��0����
�֡�������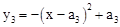 ��x�ύ��A2��6��0������D(6�Da3)2+a3=0����a3=4��9��
��x�ύ��A2��6��0������D(6�Da3)2+a3=0����a3=4��9��
��a3> a3����a3=4����ȥ������a3=9����������y3�Ķ�������Ϊ��9��9����
��������y1�Ķ�������Ϊ��1��1����y2�Ķ�������Ϊ��4��4����y3�Ķ�������Ϊ��9��9������������������yn�Ķ�������Ϊ��n2��n2����
�����������ߵĶ���ĺ�������������꣬
�ඥ����������ĺ�����ϵʽ�ǣ�y= x��
��3�����ɣ�2����֪A0A1=2��A1A2=4��A2A3=6����A n��1 A n=2 n��
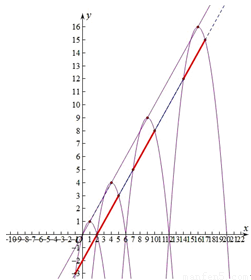
�ڲ²�������ֱ��y=xƽ���ҹ�A��2��0����һ��ֱ�ߣ���y=x��2��
��������ֵ����֤��ȡ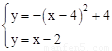 ��
��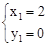 ��
��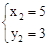 �������صõ��߶γ���Ϊ
�������صõ��߶γ���Ϊ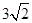 ����һ�����������ԣ������ֵҲΪ
����һ�����������ԣ������ֵҲΪ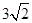 ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��֪������y=-x2+mx-n�ĶԳ���Ϊx=-2������x��ֻ��һ�����㣮
��֪������y=-x2+mx-n�ĶԳ���Ϊx=-2������x��ֻ��һ�����㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| 2 |
| 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
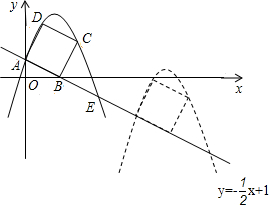
 ��֪������y=ax2+bx+c����C��0��3��������P��2��-1����ֱ��x=m��m��3����x���ڵ�D�������߽�x����A��B���㣨��ͼ10����
��֪������y=ax2+bx+c����C��0��3��������P��2��-1����ֱ��x=m��m��3����x���ڵ�D�������߽�x����A��B���㣨��ͼ10�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| b |
| 2a |
| 4ac-b2 |
| 4a |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com