
【题目】如图,△ABC≌△DEB,点E在AB上,DE与AC相交于点F.
(1)当DE=8,BC=5时,线段AE的长为____;
(2)若∠D=35°,∠C=60°,求∠DBC的度数.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】教材第九章中探索乘法公式时,设置由图形面积的不同表示方法验证了乘法公式.我国著名的数学家赵爽,早在公元3世纪,就把一个矩形分成四个全等的直角三角形,用四个全等的直角三角形拼成了一个大的正方形(如图①),这个图形称为赵爽弦图,验证了一个非常重要的结论:在直角三角形中两直角边a、b与斜边c满足关系式a2+b2=c2,称为勾股定理.
(1)爱动脑筋的小明把这四个全等的直角三角形拼成了另一个大的正方形(如图②),也能验证这个结论,请你帮助小明完成验证的过程.
(2)小明又把这四个全等的直角三角形拼成了一个梯形(如图③),利用上面探究所得结论,求当a=3,b=4时梯形ABCD的周长.
(3)如图④,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.请在图中画出△ABC的高BD,利用上面的结论,求高BD的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC和△A1B1C1关于点E成中心对称.

(1)画出对称中心E,并写出点E、A、C的坐标;
(2)P(a,b)是△ABC的边AC上一点,△ABC经平移后点P的对应点为P2(a+6,b+2),请画出上述平移后的△A2B2C2,并写出点A2、C2的坐标;
(3)判断△A2B2C2和△A1B1C1的位置关系(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y= ![]() (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(m≠0)的图象交于点A(3,1),且过点B(0,﹣2).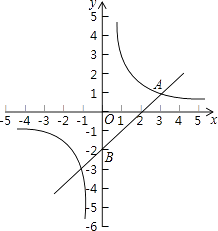
(1)求反比例函数和一次函数的表达式;
(2)如果点P是x轴上一点,且△ABP的面积是3,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂加工一批零件,为了提高工人工作积极性,工厂规定每名工人每次薪金如下:生产的零件不超过a件,则每件3元,超过a件,超过部分每件b元,如图是一名工人一天获得薪金y(元)与其生产的件数x(件)之间的函数关系式,则下列结论错误的是( ) 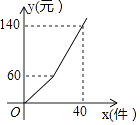
A.a=20
B.b=4
C.若工人甲一天获得薪金180元,则他共生产50件
D.若工人乙一天生产m(件),则他获得薪金4m元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(5,3)、B(5,1). 
(1)在图中标出△ABC外心D的位置,并直接写出它的坐标;
(2)判断△ABC的外接圆D与x轴、y轴的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张买了张![]() 元的乘车IC卡,如果他乘车的次数用
元的乘车IC卡,如果他乘车的次数用![]() 表示,则记录他每次乘车后的余额
表示,则记录他每次乘车后的余额![]() (元)如下表:
(元)如下表:
次数m | 余额n(元) |
1 | 50—0.8 |
2 | 50—1.6 |
3 | 50—2.4 |
4 | 50—3.2 |
…… | …… |
【1】⑴写出乘车的次数![]() 表示余额
表示余额![]() (元)的关系式;
(元)的关系式;
【2】⑵利用上述关系式计算小张乘了13次车后还剩下多少元?
【3】⑶小张最多能乘几次车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两点A、B对应的数分别为![]() ,4,点P为数轴上一动点,其对应的数为x
,4,点P为数轴上一动点,其对应的数为x
![]() 若点P到点A、点B的距离相等,求点P对应的数
若点P到点A、点B的距离相等,求点P对应的数
![]() 数轴上是否存在点P,使点P到点A、点B的距离之和为7?若存在,请直接写出x的值
数轴上是否存在点P,使点P到点A、点B的距离之和为7?若存在,请直接写出x的值![]() 若不存在,请说明理由?
若不存在,请说明理由?
![]() 若点P以1个单位
若点P以1个单位![]() 的速度从点O向右运动,同时点A以5个单位
的速度从点O向右运动,同时点A以5个单位![]() 的速度向左运动,点B以20个单位
的速度向左运动,点B以20个单位![]() 的速度向右运动,在运动过程中,M、N分别是AP、OB的中点,问:
的速度向右运动,在运动过程中,M、N分别是AP、OB的中点,问:![]() 的值是否发生变化?请说明理由.
的值是否发生变化?请说明理由.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com