Question

16．如图，抛物线y=ax²+bx+c（a≠0）与x轴交于点A（-1，0），B（3，0）两点，与y轴交于点 C（0，-3）．
（1）求该抛物线的解析式及顶点M的坐标；
（2）求△BCM的面积；
（3）若P是 x轴上一个动点，过P作射线PQ∥AC交抛物线于点Q，随着P点的运动，在抛物线上是否存在这样的点Q，使以A、P、Q、C为顶点的四边形为平行四边形？若存在请求出Q点的坐标；若不存在，请说明理由．

Answer 1

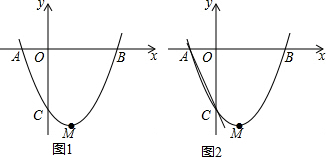
分析 （1）根据A（-1，0），B（3，0），C（0，-3），设抛物线解析式为y=a（x+1）（x-3），代入（0，-3），解方程即可得出抛物线解析式，进而得到顶点M的坐标；
（2）连BC、BM、CM，作MD⊥轴于D，根据S_△BCM=S_梯形OCMD+S_△BMD-S_△BCO进行计算即可；
（3）分两种情形讨论：①当Q点在x轴下方时，作QE⊥x轴于E；②当Q点在x轴上方时，作QF⊥x轴于F，分别根据Q的纵坐标，求出点Q的横坐标即可．

解答 解：（1）设抛物线解析式为y=a（x+1）（x-3），
∵抛物线过点 C（0，-3），
∴-3=a（0+1）（0-3），
∴a=1，
∴抛物线解析式为 y=（x+1）（x-3），
∵y=（x+1）（x-3）=（x-1）²-4，
∴M（1，-4）；

（2）如图1，连BC、BM、CM，作MD⊥轴于D，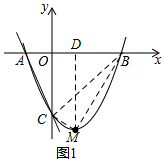

∴S_△BCM=S_梯形OCMD+S_△BMD-S_△BCO
=$\frac{1}{2}$（3+4）×1+$\frac{1}{2}$×2×4-$\frac{1}{2}$×3×3
=$\frac{7}{2}$+4-$\frac{9}{2}$
=3；

（3）存在这样的点Q，使以A、P、Q、C为顶点的四边形为平行四边形．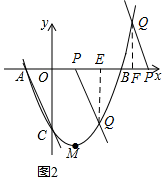

①如图2，当Q点在轴下方时，作QE⊥轴于E，
∵AC∥PQ且AC=PQ，
∴OC=EQ=3，
当-3=x²-2x-3时，
解得：x₁=0（舍），x₂=2，
∴Q（2，-3）；
②如图2，当Q点在 轴上方时，作QF⊥轴于F，
∵AC∥PQ且AC=PQ，
∴Rt△OAC≌Rt△FPQ，
∴OC=FQ=3，
当3=x²-2x-3时，
解得：x₁=1-$\sqrt{7}$，x₂=1+$\sqrt{7}$，
∴Q（1-$\sqrt{7}$，3）或（1+$\sqrt{7}$，3），
综上所述，满足条件的Q点为（2，-3）或（1-$\sqrt{7}$，3）或（1+$\sqrt{7}$，3）．

点评 本题属于二次函数综合题，主要考查了三角形面积、平行线的性质，全等三角形的判定和性质以及解一元二次方程的综合应用，解题的关键是灵活应用待定系数法确定函数解析式，学会利用分割法求三角形的面积，学会分类讨论的思想解决问题．