
分析 (1)配方法求解可得;
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:(1)∵x2-2x=1,
∴x2-2x+1=1+1,即(x-1)2=2,
∴x-1=±$\sqrt{2}$,
则x=1$±\sqrt{2}$;
(2)解不等式x+1≥$\frac{x}{2}$,得:x≥-2,
解不等式2x+6>3x+2,得:x<4,
则不等式组的解集为-2≤x<4.
点评 本题考查的是解一元二次方程和解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
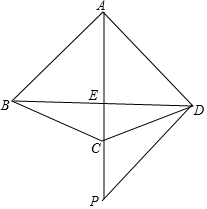 如图,四边形ABCD中,AB=AC=AD,AC平分∠BAD,点P是AC延长线上一点,且PD⊥AD.
如图,四边形ABCD中,AB=AC=AD,AC平分∠BAD,点P是AC延长线上一点,且PD⊥AD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
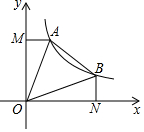 如图,一次函数y=-x+b(b>0)的图象与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A、B两点,连接OA、OB,AM⊥y轴,BN⊥x轴,垂足分别为M、N.下列结论:
如图,一次函数y=-x+b(b>0)的图象与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A、B两点,连接OA、OB,AM⊥y轴,BN⊥x轴,垂足分别为M、N.下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
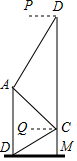 如图,某中学在教学楼前新建了一座雕塑AB,为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角∠QCA为45°,底部点B的俯角∠QCB为30°,小华在五楼找到一点D,利用三角尺测得点A的俯角∠PDA为60°,若AD为8m,则雕塑AB的高度为多少?(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.73).
如图,某中学在教学楼前新建了一座雕塑AB,为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角∠QCA为45°,底部点B的俯角∠QCB为30°,小华在五楼找到一点D,利用三角尺测得点A的俯角∠PDA为60°,若AD为8m,则雕塑AB的高度为多少?(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.73).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
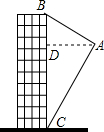 如图,航拍无人机从点A处测得一幢建筑物顶部B的仰角为32°,测得底部C的仰角为62°,此时航拍无人机与该建筑物的水平距离AD为54米,求该建筑物的高度BC(精确到0.1米,参考数据:sin 32°=0.530,cos32°=0.848,tan32°=0.625,sin 62°=0.883,cos62°=0.469,tan62°=1.88)
如图,航拍无人机从点A处测得一幢建筑物顶部B的仰角为32°,测得底部C的仰角为62°,此时航拍无人机与该建筑物的水平距离AD为54米,求该建筑物的高度BC(精确到0.1米,参考数据:sin 32°=0.530,cos32°=0.848,tan32°=0.625,sin 62°=0.883,cos62°=0.469,tan62°=1.88)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
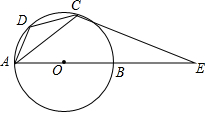 如图,AB为⊙O的直径,AD为弦,过⊙O上一点C作⊙O的切线交AB的延长线于E,且∠DCA=∠E.
如图,AB为⊙O的直径,AD为弦,过⊙O上一点C作⊙O的切线交AB的延长线于E,且∠DCA=∠E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
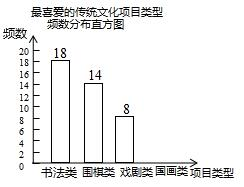 某校为更好地培养学生兴趣,开展“拓展课程走班选课”活动,随机抽查了部分学生,了解他们最喜爱的项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.
某校为更好地培养学生兴趣,开展“拓展课程走班选课”活动,随机抽查了部分学生,了解他们最喜爱的项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.| 项目类型 | 频数 | 频率 |
| 书法类 | 18 | a |
| 围棋类 | 14 | 0.28 |
| 喜剧类 | 8 | 0.16 |
| 国画类 | b | 0.20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
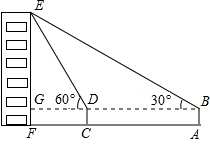 如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.($\sqrt{3}$=1.732,结果精确到0.1米)
如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.($\sqrt{3}$=1.732,结果精确到0.1米)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com