
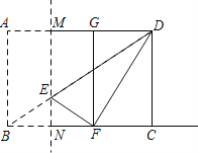
【题目】 如图,在矩形ABCD中,点N为边BC上不与B、C重合的一个动点,过点N作MN⊥BC交AD于点M,交BD于点E,以MN为对称轴折叠矩形ABNM,点A、B的对应点分别是G、F,连接EF、DF,若AB=6,BC=8,当△DEF为直角三角形时,CN的长为______.
【答案】![]() 或
或![]()
【解析】
△DEF为直角三角形时,可能出现三种情况,分别令不同的内角为直角,画出相应的图形,根据折叠的性质和相似三角形的性质进行解答即可.
解:矩形ABCD中,AB=6,BC=8,
∴BD=![]() =10,
=10,
由折叠得:BE=EF,BN=NF,∠EBF=∠EFB,∠BEN=∠FEN,
当△DEF为直角三角形时,
(1)当∠DEF=90°,则∠BEN=∠FEN=45°,不合题意;
(2)当∠EFD=90°时,如图1所示:
∵∠EFN+∠DFC=90°,∠DFC+∠CDF=90°,
∴∠EFN=∠CDF=∠EBN,
∵tan∠DBC=![]() =
=![]() =tan∠CDF=
=tan∠CDF=![]()
设CN=x,则BN=NF=8-x,FC=x-(8-x)=2x-8,
∴![]() =
=![]()
解得:x=![]() ,即CN=
,即CN=![]() .
.
(3)当∠EDF=90°时,如图2所示:
易证△BDC∽△DFC,
∴CD2=BCCF
设CN=x,则BN=NF=8-x,FC=(8-x)-x=8-2x,
∴62=8(8-2x)
解得:x=![]() ,即CN=
,即CN=![]() ,
,
综上所述,CN的长为![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.



 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
【题目】 有四张正面分别标有数字1,2,-3,-4的不透明卡片,它们除了数字之外其余全部相同,将它们背面朝上,洗匀后从四张卡片中随机地抽取一张不放回,将该卡片上的数字记为m,再随机地抽取一张,将卡片上的数字记为n.
(1)请用画树状图或列表法写出(m,n)所有的可能情况;
(2)求所选的m,n能使一次函数y=mx+n的图象经过第一、三、四象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有3000名学生.为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E | F |
上学方式 | 电动车 | 私家车 | 公共交通 | 自行车 | 步行 | 其他 |
某校部分学生主要上学方式扇形统计图某校部分学生主要上学方式条形统计图
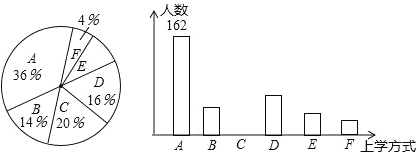
根据以上信息,回答下列问题:
(1)参与本次问卷调查的学生共有____人,其中选择B类的人数有____人.
(2)在扇形统计图中,求E类对应的扇形圆心角α的度数,并补全条形统计图.
(3)若将A、C、D、E这四类上学方式视为“绿色出行”,请估计该校每天“绿色出行”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
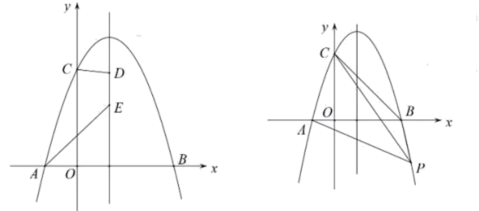
【题目】如图所示抛物线![]() 过点
过点![]() ,点
,点![]() ,且
,且![]()
(1)求抛物线的解析式及其对称轴;
(2)点![]() 在直线
在直线![]() 上的两个动点,且
上的两个动点,且![]() ,点
,点![]() 在点
在点![]() 的上方,求四边形
的上方,求四边形![]() 的周长的最小值;
的周长的最小值;
(3)点![]() 为抛物线上一点,连接
为抛物线上一点,连接![]() ,直线
,直线![]() 把四边形
把四边形![]() 的面积分为3∶5两部分,求点
的面积分为3∶5两部分,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
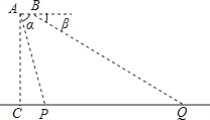
【题目】如图,为了测量一座大桥的长度,在一架水平飞行的无人机AB的尾端A点测得桥头P点的俯角α=74°,前端B点测得桥尾Q点的俯角=30°,此时无人机的飞行高度AC=868米,AB=1米.求这座大桥PQ的长度(结果保留整数)(参考数据:sin74°≈0.9,cos74°≈0.3,tan74°≈3.5,![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,四边形ABCD内接于以BC为直径的圆,圆心为O,且AB=AD,延长CB、DA交于P,过C点作PD的垂线交PD的延长线于E,且PB=BO,连接OA.
(1)求证:OA∥CD;
(2)求线段BC:DC的值;
(3)若CD=18,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
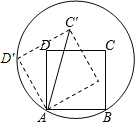
【题目】如图,边长为2的正方形ABCD的顶点A、B在一个半径为2的圆上,顶点C、D在该圆内.将正方形ABCD绕点A逆时针旋转,当点D第一次落在圆上时,点C旋转到C′,则∠C′AB=__°.
查看答案和解析>>
科目:初中数学 来源: 题型:
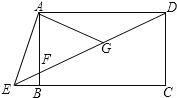
【题目】如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,2∠CED=∠AED,点G是DF的中点
(1)求证:∠CED=∠DAG;
(2)若AG=4,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天晚上,小颖由路灯A下的B处向正东走到C处时,测得影子CD的长为1米.当她继续向正东走到D处时,测得此时影子DE的一端E到路灯A的仰角为45°.已知小颖的身高为1.5米,那么路灯AB的高度是多少米?( )

A.4米B.4.5米C.5米D.6米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com