练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】甲乙两地相距200km，快车速度为120 ，慢车速度为80 ，慢车从甲地出发，快车从乙地出发，

    （1）如果两车同时出发，相向而行，出发后几时两车相遇？相遇时离甲地多远？

    （2）如果两车同时出发，同向（从乙开始向甲方向）而行，出发后几时两车相遇?

    【答案】（1）1小时，80km；（2）5小时.

    【解析】试题分析：

    (1)相遇问题，设 小时后两车相遇，则两车行驶距离之和为甲乙两地距离；

    (2)追及问题，设小时后两车相遇，则两车行驶距离之差为甲乙两地距离；

    试题解析：(1)设小时后两车相遇，则

    由题意， ，

    解之，得 ，

    故1小时后两车相遇，相遇时离甲地80 km .

    (2)设 小时后两车相遇，则

    由题意， ，

    解之，得 ，

    故5小时后两车相遇.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知直线l与直线l外一点P，求作：过点P且垂直于直线l的垂线a（尺规作图）．

    现给出一种作法，如下：

    步骤一：在直线l外取一点E，以点P为圆心，以线段PE为半径画弧，交直线l于点M，N；

    步骤二：分别以点M、N为圆心，大于线段MN为半径画弧，过两弧的交点的直线a就是所求作的垂线．

    （1）按上述操作步骤，请成功作出过点P且垂直于直线l的垂线a．（符合要求的一种图形），并说明理由．

    （2）从你作图的过程中，思考要保证这种作法顺利作出，线段PE应该满足什么条件？

    （3）为了避免这种情况产生，小明说只要在直线l上取点E好了，并给出了画法，画法对吗？请说明理由．

    （作法：在直线l上取两点B、D，以P为圆心，以PD 为半径画圆交直线l于点E，以P为圆心，以PB 为半径画圆交直线l于点F，其中较小圆分别交PB，PF于点M、N，连接E、N和D、M，EN和MD相交于点H，则PH就是所求的垂线．）

    （4）请在直线l上取点E，用直尺和圆规过点P且垂直于直线l的垂线a（与小明不同的方法，并要求尽可能简单）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线 y= x2﹣2x的顶点是A，与x轴相交于点B、C两点（点B在点C的左侧）．
    （1）求A、B、C的坐标；
    （2）直接写出当y＜0时x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某工厂与A、B两地有公路、铁路相连．这家工厂从A地购买一批每吨2000元的原料运回工厂，制成每吨7500元的产品运到B地．已知公路运价为2元/ (吨·千米)，铁路运价为 1.5元/(吨·千米)，且这两次运输共支出公路运输费2.6万元，铁路运输费15.6万元。

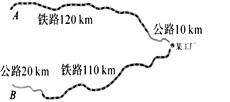
    求：(1)该工厂从A地购买了多少吨原料？ 制成运往B地的产品多少吨？

    (2)若不计人力成本，这批产品盈利多少元？ （盈利=销售款-原料费-运输费）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=﹣x2﹣2x+3与x轴交于A、B两点，与y轴交于点C．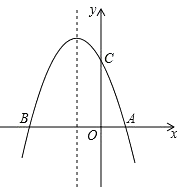

    （1）求B、C两点的坐标；
    （2）在该抛物线的对称轴上是否存在点P，使得△PAC的周长最小？若存在，求出点P的坐标；若不存在，请说明理由；
    （3）抛物线在第二象限内是否存在一点Q，使△QBC的面积最大？，若存在，求出点Q的坐标及△QBC的面积最大值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：
    ①4ac＜b2；
    ②方程ax2+bx+c=0的两个根是x1=﹣1，x2=3；
    ③3a+c＞0
    ④当y＞0时，x的取值范围是﹣1≤x＜3
    ⑤当x＜0时，y随x增大而增大
    其中结论正确的个数是（ ）

    A.4个
    B.3个
    C.2个
    D.1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）若a－b＝1，则代数式a2－b2－2b的值为____．

    （2）若m＋n＝4，mn＝5，则多项式m3n2＋m2n3的值是____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】方程x2﹣3x﹣5=0的根的情况是（ ）
    A.有两个不相等的实数根
    B.有两个相等的实数根
    C.没有实数根
    D.无法确定是否有实数根

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】①平行四边形，②矩形，③菱形，④正方形中，对角线的交点到各边中点的距离都相等的是（ ）

    A. ①② B. ③④ C. ②③ D. ②④

    查看答案和解析>>

    同步练习册答案