Question

7．如图，在△ABC中，AB=AC，∠BAC=90°，∠ABD=30°，AB=BD，求证：AD=DC．

Answer 1

分析 求出∠BAD=∠BDA=75°，构造△ABE，E′在△ABC内部，使得AE=AD，∠ABE=∠DBE=15°，连DE，根据全等三角形的判定证△DBE≌△ABE，求出∠BAE=∠CAD，根据全等三角形的判定求出△BAE≌△CAD，根据全等得出∠ABE=∠ACD=15°，求出∠CAD=∠ACD=15°，即可得出答案．

解答 解：∵∠ABD=30°，AB=BD，
∴∠BAD=∠BDA=75°，
如图，构造△ABE，E′在△ABC内部，使得AE=AD，∠ABE=∠DBE=15°，连DE，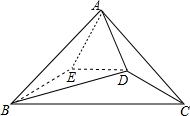

∵在△DBE和△ABE中
$\left\{\begin{array}{l}{DB=AB}\\{∠ABE=∠DBE}\\{BE=BE}\end{array}\right.$
∴△DBE≌△ABE，
∴AE=DE，
∵AE=AD，
∴△AED是等边三角形，
∴∠EAD=∠ADE=60°，
∴∠BAE=∠BDE=75°-60°=15°，
∴∠CAD=90°-75°=15°，
∴∠BAE=∠CAD，
在△BAE和△CAD中
$\left\{\begin{array}{l}{AE=AD}\\{∠BAE=∠CAD}\\{AB=AC}\end{array}\right.$
∴△BAE≌△CAD（SAS），
∴∠ABE=∠ACD=15°，
∵∠CAD=15°，
∴∠CAD=∠ACD=15°，
∴AD=DC．

点评 本题考查了全等三角形的性质定理与判定定理，解决本题的关键是构建全等三角形．