
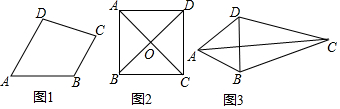
 平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD,AB的中点.下列结论:①EG=EF; ②△EFG≌△GBE; ③FB平分∠EFG;④EA平分∠GEF;⑤四边形BEFG是菱形.其中正确的是①②④.
平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD,AB的中点.下列结论:①EG=EF; ②△EFG≌△GBE; ③FB平分∠EFG;④EA平分∠GEF;⑤四边形BEFG是菱形.其中正确的是①②④. 分析 由中点的性质可得出EF∥CD,且EF=$\frac{1}{2}$CD=BG,结合平行即可证得②结论成立,由BD=2BC得出BO=BC,即而得出BE⊥AC,由中线的性质可知GP∥BE,且GP=$\frac{1}{2}$BE,AO=EO,通过证△APG≌△EPG得出AG=EG=EF得出①成立,再证△GPE≌△FPE得出④成立,此题得解.
解答 解:令GF和AC的交点为点P,如图所示: ∵E、F分别是OC、OD的中点,
∵E、F分别是OC、OD的中点,
∴EF∥CD,且EF=$\frac{1}{2}$CD,
∵四边形ABCD为平行四边形,
∴AB∥CD,且AB=CD,
∴∠FEG=∠BGE(两直线平行,内错角相等),
∵点G为AB的中点,
∴BG=$\frac{1}{2}$AB=$\frac{1}{2}$CD=FE,
在△EFG和△GBE中,$\left\{\begin{array}{l}{BG=FE}&{\;}\\{∠FEG=∠BGE}&{\;}\\{GE=EG}&{\;}\end{array}\right.$,
∴△EFG≌△GBE(SAS),即②成立,
∴∠EGF=∠GEB,
∴GF∥BE(内错角相等,两直线平行),
∵BD=2BC,点O为平行四边形对角线交点,
∴BO=$\frac{1}{2}$BD=BC,
∵E为OC中点,
∴BE⊥OC,
∴GP⊥AC,
∴∠APG=∠EPG=90°
∵GP∥BE,G为AB中点,
∴P为AE中点,即AP=PE,且GP=$\frac{1}{2}$BE,
在△APG和△EGP中,$\left\{\begin{array}{l}{AP=EP}&{\;}\\{∠APG=∠EPG}&{\;}\\{GP=GP}&{\;}\end{array}\right.$,
∴△APG≌△EPG(SAS),
∴AG=EG=$\frac{1}{2}$AB,
∴EG=EF,即①成立,
∵EF∥BG,GF∥BE,
∴四边形BGFE为平行四边形,
∴GF=BE,
∵GP=$\frac{1}{2}$BE=$\frac{1}{2}$GF,
∴GP=FP,
∵GF⊥AC,
∴∠GPE=∠FPE=90°
在△GPE和△FPE中,$\left\{\begin{array}{l}{GP=FP}&{\;}\\{∠GPE=∠FPE}&{\;}\\{EP=EP}&{\;}\end{array}\right.$,
∴△GPE≌△FPE(SAS),
∴∠GEP=∠FEP,
∴EA平分∠GEF,即④成立.
故答案为:①②④.
点评 本题考查了全等三角形的判定与性质、中位线定理以及平行线的性质定理,解题的关键是利用中位线,寻找等量关系,借助于证明全等三角形找到边角相等.


科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| α | 30° | 45° | 60° |
| sinα | |||
| cosα | |||
| tanα |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{2}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
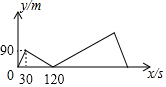 甲、乙两人在1800米长的直线道路上跑步,甲、乙两人同起点、同方向出发,并分别以不同的速度匀速前进.已知,甲出发30秒后,乙出发,乙到终点后立即返回,并以原来的速度前进,最后与甲相遇,此时跑步结束.如图,y(米)表示甲、乙两人之间的距离,t(秒)表示甲出发的时间,图中折线及数据表示整个跑步过程中y与t函数关系.那么,乙到终点后$\frac{360}{7}$秒与甲相遇.
甲、乙两人在1800米长的直线道路上跑步,甲、乙两人同起点、同方向出发,并分别以不同的速度匀速前进.已知,甲出发30秒后,乙出发,乙到终点后立即返回,并以原来的速度前进,最后与甲相遇,此时跑步结束.如图,y(米)表示甲、乙两人之间的距离,t(秒)表示甲出发的时间,图中折线及数据表示整个跑步过程中y与t函数关系.那么,乙到终点后$\frac{360}{7}$秒与甲相遇.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.201×10-4 | B. | 2.01×10-6 | C. | 20.1×10-6 | D. | 2.01×10-5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com