
分析 (1)设一件B型商品的进价为x元,则一件A型商品的进价为(x+10)元.根据16000元采购A型商品的件数是用7500元采购B型商品的件数的2倍,列出方程即可解决问题;
(2)根据总利润=两种商品的利润之和,列出式子即可解决问题;
(3)设利润为w元.则w=(80-a)m+70(250-m)=(10-a)m+17500,分三种情形讨论即可解决问题.
解答 解:(1)设一件B型商品的进价为x元,则一件A型商品的进价为(x+10)元.
由题意:$\frac{16000}{x+10}$=$\frac{7500}{x}$×2,
解得x=150,
经检验x=150是分式方程的解,
答:一件B型商品的进价为150元,则一件A型商品的进价为160元.
(2)因为客商购进A型商品m件,所以客商购进B型商品(250-m)件.
由题意:v=80m+70(250-m)=10m+17500,
∵80≤m≤250-m,
∴80≤m≤125,
(3)设利润为w元.则w=(80-a)m+70(250-m)=(10-a)m+17500,
①当10-a>0时,w随m的增大而增大,所以m=125时,最大利润为(18750-125a)元.
②当10-a=0时,最大利润为17500元.
③当10-a<0时,w随m的增大而减小,所以m=80时,最大利润为(18300-80a)元.
点评 本题考查分式方程的应用、一次函数的应用等知识,解题的关键是理解题意,学会构建方程或一次函数解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
 如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1,还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2017次操作后得到的折痕D2016E2016,到BC的距离记为h2017;若h1=1,则h2017的值为2-$\frac{1}{{2}^{2016}}$.
如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1,还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2017次操作后得到的折痕D2016E2016,到BC的距离记为h2017;若h1=1,则h2017的值为2-$\frac{1}{{2}^{2016}}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 宏兴企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系:y=$\left\{\begin{array}{l}7.5x({0≤x≤4})\\ 5x+10({4<x≤14})\end{array}$.
宏兴企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系:y=$\left\{\begin{array}{l}7.5x({0≤x≤4})\\ 5x+10({4<x≤14})\end{array}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
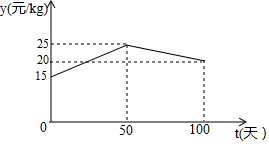 湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了20000kg淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养10天的总成本为30.4万元;放养20天的总成本为30.8万元(总成本=放养总费用+收购成本).
湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了20000kg淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养10天的总成本为30.4万元;放养20天的总成本为30.8万元(总成本=放养总费用+收购成本).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
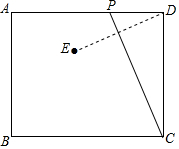 如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s).
如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
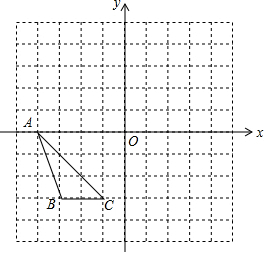 如图,在边长为1的正方形网格中,△ABC的顶点均在格点上.
如图,在边长为1的正方形网格中,△ABC的顶点均在格点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com