
 △ABC中,AD⊥BC,垂足为D,作DE⊥AB,DF⊥AC,连结EF,求证:∠ABC=∠AFE.
△ABC中,AD⊥BC,垂足为D,作DE⊥AB,DF⊥AC,连结EF,求证:∠ABC=∠AFE. 分析 由垂线的定义得出∠ADB=90°,∠DEA=90°,由角的互余关系得出∠ABC=∠ADE,再证明A、E、D、F四点共圆,由圆周角定理得出∠AFE=∠ADE,即可得出∠ABC=∠AFE.
解答 证明:如图所示:
∵AD⊥BC,DE⊥AB,
∴∠ADB=90°,∠DEA=90°,
∴∠ABC+∠BAD=90°,∠BAD+∠ADE=90°,
∴∠ABC=∠ADE,
∵DF⊥AC,
∴∠DFA=90°,
∴∠DEA+∠DFA=180°,
∴A、E、D、F四点共圆,
∴∠AFE=∠ADE,
∴∠ABC=∠AFE.
点评 本题是四点共圆题目,考查了四点共圆、圆周角定理、垂线的定义、角的互余关系等知识;本题综合性强,难度适中,证明四点共圆是解决问题的关键.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:解答题
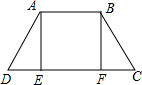 如图所示,四边形ABCD是一条河堤坝的横截面,AE=BF,且AE⊥CD,BF⊥CD,垂足分别为E、F,AD=BC,∠C与∠D是否相等?为什么?
如图所示,四边形ABCD是一条河堤坝的横截面,AE=BF,且AE⊥CD,BF⊥CD,垂足分别为E、F,AD=BC,∠C与∠D是否相等?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6cm2 | B. | 16cm2 | C. | 64cm2 | D. | 81cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在同一平面内,圆O和直线AB相切,P是圆O上一个定点,初始位置圆O和AB相切于点A(此时点P与点A重合),从A处开始圆O在直线AB上以每3分钟1圈的速度匀速向右无滑动地滚动,1分钟到达点E(圆O与AB相切于点E),此时,tan∠PAE的值为$\frac{9}{4π-3\sqrt{3}}$.
如图,在同一平面内,圆O和直线AB相切,P是圆O上一个定点,初始位置圆O和AB相切于点A(此时点P与点A重合),从A处开始圆O在直线AB上以每3分钟1圈的速度匀速向右无滑动地滚动,1分钟到达点E(圆O与AB相切于点E),此时,tan∠PAE的值为$\frac{9}{4π-3\sqrt{3}}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲车从A地出发,途径C地时休息一小时,然后按原速度继续前进到达B地;乙车从C地出发到B地后又按原速返回C地,两车同时出发,并以各自的速度匀速行驶,设A,C,B在同一条直线上,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.
甲车从A地出发,途径C地时休息一小时,然后按原速度继续前进到达B地;乙车从C地出发到B地后又按原速返回C地,两车同时出发,并以各自的速度匀速行驶,设A,C,B在同一条直线上,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com