
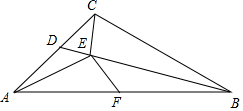
 如图,等腰直角△ABC中,F为斜边AB的中点,D为AC上一点,连接BD,作CE⊥BD,垂足为E,连接AE,EF,若∠AEF=90°,求证:EF2=DE•CE.
如图,等腰直角△ABC中,F为斜边AB的中点,D为AC上一点,连接BD,作CE⊥BD,垂足为E,连接AE,EF,若∠AEF=90°,求证:EF2=DE•CE. 分析 从所要证明的结论形式上看,需要借助相似三角形来解决问,注意到F是AB中点,于是连接FC,先证△AEB∽△FEC,可得$EF=\frac{CE•AE}{BE}$,再证△ADE∽△BFE,得到$EF=\frac{DE•EB}{AE}$,两式相乘即是结论.
解答 证明:如图,连接FC,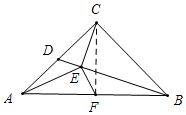
∵△ACB是等腰直角三角形,F为斜边AB中点,
∴CF⊥AB,CF=AF=BF,
∵CE⊥BD,
∴∠CEB=∠CFB=90°,
∴C、E、F、B四点共圆,
∴∠ECF=∠EBA,
∵∠AEF=90°,
∴∠AEB=∠FEC,
∴△AEB∽△FEC,
∴$\frac{CE}{BE}=\frac{EF}{AE}$,
∴$EF=\frac{CE•AE}{BE}$,①
∵C、E、F、B四点共圆,
∴∠FEB=∠FCB=45°,
∴∠AED=180°-90°-45°=45°,
∵∠CAE+∠CFE=∠CFA+∠CAF-∠EFA-∠EAF=45°,
∠CFE+∠EBF=∠CBE+∠EBF=45°,
∴∠DAE=∠EBF,
∴△ADE∽△BFE,
∴$\frac{AE}{BE}=\frac{DE}{EF}$,
∴$EF=\frac{DE•EB}{AE}$,②
①×②得:EF2=DE•CE
点评 本题主要考查了等腰直角三角形的性质、四点共圆的判定与性质、相似三角形的判定与性质等知识点,有一定难度.推导图中的角度关系,从而相似三角形的判定提供条件是本题的关键也是难点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
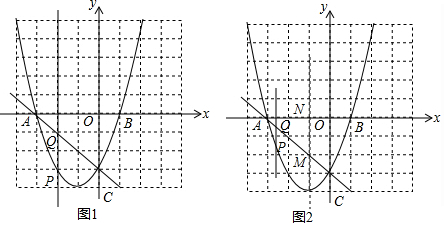
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com