
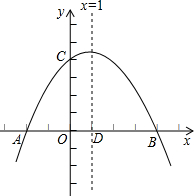 (2010•毕节地区)如图在平面平面直角系中,抛物线y=ax2+bx+c(a≠0)的图象与轴交于点A(-2,0)、B(4,0),与轴交于点C(0,4),直线l是抛物线的对称轴,与x轴交于点D,点P是直线l上一动点.
(2010•毕节地区)如图在平面平面直角系中,抛物线y=ax2+bx+c(a≠0)的图象与轴交于点A(-2,0)、B(4,0),与轴交于点C(0,4),直线l是抛物线的对称轴,与x轴交于点D,点P是直线l上一动点.| 5 |
| 11 |
| 11 |
| 11 |
| 5 |
| 19 |
| 19 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 | ||
2×(-
|
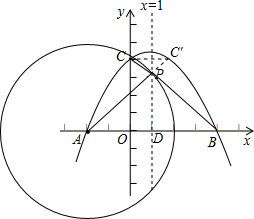
| 5 |
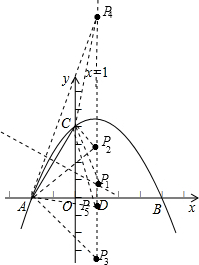 以A圆心、AC为半径交直线x=1于P2、P3,连AP2,AP3,
以A圆心、AC为半径交直线x=1于P2、P3,连AP2,AP3,(2
|
| 11 |
| 11 |
| 11 |
| 5 |
| 19 |
| 19 |
| 11 |
| 11 |
| 19 |
| 19 |


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
 (2010•毕节地区)如图方格纸中的每个小正方形都是边长为1个单位的正方形,建立平面直角坐标系后,将△ABC绕点O沿顺时针方向旋转90°后,点B的对应点B′的坐标为( )
(2010•毕节地区)如图方格纸中的每个小正方形都是边长为1个单位的正方形,建立平面直角坐标系后,将△ABC绕点O沿顺时针方向旋转90°后,点B的对应点B′的坐标为( )查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2010•毕节地区)小明准备在毕业晚会上表演戏剧需制作一顶圆锥形小丑帽,现有一张边长为30cm的正方形纸片,如图所示,沿虚线剪下来后,制作成的小丑帽的侧面积为( )(接缝出忽略不计)
(2010•毕节地区)小明准备在毕业晚会上表演戏剧需制作一顶圆锥形小丑帽,现有一张边长为30cm的正方形纸片,如图所示,沿虚线剪下来后,制作成的小丑帽的侧面积为( )(接缝出忽略不计)查看答案和解析>>
科目:初中数学 来源: 题型:
 (2010•毕节地区)如图,小红用灯泡O照射三角尺ABC,在墙上形成影子△A′B′C′.现测得OA=5cm,
(2010•毕节地区)如图,小红用灯泡O照射三角尺ABC,在墙上形成影子△A′B′C′.现测得OA=5cm,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com