
如图,一次函数y=-x+b与反比例函数 的图象相交于A(-1,4)、B(4,-1)两点,直线l⊥x轴于点E(-4,0),与反比例函数和一次函数的图象分别相交于点C、D,连接AC、BC
的图象相交于A(-1,4)、B(4,-1)两点,直线l⊥x轴于点E(-4,0),与反比例函数和一次函数的图象分别相交于点C、D,连接AC、BC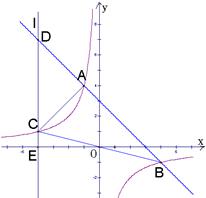
(1)、求出b和k;
(2)、求证:△ACD是等腰直角三角形;
(3)、在y轴上是否存在点P,使 ,若存在,请求出P的坐标,若不存在,请说明理由。
,若存在,请求出P的坐标,若不存在,请说明理由。
(1)3,-4;(2)证明见解析;(3)存在,P1(0,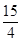 ),P2(0,-
),P2(0,-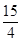 ).
).
解析试题分析:(1)将已知点的坐标代入到两个函数的解析式即可求得k和b的值;
(2))根据直线x=-4与一次函数y=-x+3交于点D,求得点D(-4,7),根据直线x=-4与反比例函数y=-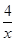 交于点C确定点C(-4,1),从而确定AD=AC,然后根据勾股定理的逆定理确定△ACD是直角三角形,从而确定△ACD是等腰直角三角形;
交于点C确定点C(-4,1),从而确定AD=AC,然后根据勾股定理的逆定理确定△ACD是直角三角形,从而确定△ACD是等腰直角三角形;
(3)过点A作AP1∥BC,交y轴于P1,则S△PBC=S△ABC,根据B(4,-1),C(-4,1)确定直线BC的解析式为y=- x,然后设直线AP1的解析式为y=-
x,然后设直线AP1的解析式为y=- x+b1,把A(-1,4)代入可求b1=
x+b1,把A(-1,4)代入可求b1=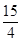 ,求得P1(0,
,求得P1(0,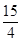 ),作P1关于x轴的对称点P2,利用S△P1BC=S△P2BCBC=S△ABC,确定P2(0,-
),作P1关于x轴的对称点P2,利用S△P1BC=S△P2BCBC=S△ABC,确定P2(0,-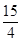 );
);
试题解析:(1)解:∵一次函数y=-x+b的图象经过点A(-1,4)
∴-(-1)+b=4,
即b=3,
又∵反比例函数 (k≠0)的图象经过点A(-1,4)
(k≠0)的图象经过点A(-1,4)
∴k=xy=(-1)×4=-4;
(2)证明:∵直线l⊥x轴于点E(-4,0)则直线l解析式为x=-4,
∴直线x=-4与一次函数y=-x+3交于点D,则D(-4,7)
直线x=-4与反比例函数y=-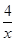 交于点C,
交于点C,
则C(-4,1)
过点A作AF⊥直线l于点F,
∵A(-1,4),C(-4,1),D(-4,7)
∴CD=6,AF=3,DF=3,FC=3
又∵∠AFD=∠AFC=90°,
由勾股定理得:AC=AD=3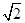
又∵AD2+AC2=(3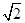 )2+(3
)2+(3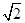 )2=36
)2=36
CD2=62=36
∴AD2+AC2=CD2
∴由勾股定理逆定理得:△ACD是直角三角形,
又∵AD=AC
∴△ACD是等腰直角三角形;
(3)解:过点A作AP1∥BC,交y轴于P1,则S△PBC=S△ABC
∵B(4,-1),C(-4,1)
∴直线BC的解析式为y=- x
x
∵设直线AP1的解析式为y=- x+b1,把A(-1,4)代入可求b1=
x+b1,把A(-1,4)代入可求b1=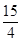 ,
,
∴P1(0,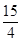 ),
),
∴作P1关于x轴的对称点P2,则S△P1BC=S△P2BCBC=S△ABC,
故P2(0,-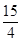 );即存在P1(0,
);即存在P1(0,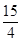 ),P2(0,-
),P2(0,-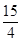 ).
).
考点: 反比例函数综合题


科目:初中数学 来源: 题型:填空题
函数yl=x(x≥0), (x>0)的图象如图所示,则结论:①两函数图象的交点A的坐标为(3,3);②当x>3时,y2>y1;③当x=1时,BC=8;④当x逐渐增大时,yl随着x的增大而增大,y2随着x的增大而减小.其中正确结论的序号是 .
(x>0)的图象如图所示,则结论:①两函数图象的交点A的坐标为(3,3);②当x>3时,y2>y1;③当x=1时,BC=8;④当x逐渐增大时,yl随着x的增大而增大,y2随着x的增大而减小.其中正确结论的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,是一辆小汽车沿一条高速公路匀速前进的时间t(小时)与速度x(千米/时)关系的图象,根据图象提供的信息回答下列问题: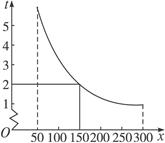
(1)这条高速公路的全长是多少千米?
(2)写出速度与时间之间的函数关系.
(3)汽车最大速度可以达到多少?
(4)汽车最慢用几个小时可以到达?如果要在3小时以内到达,汽车的速度应不少于多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,矩形OABC的顶点A、C分别在x轴和y轴上,点 的坐标为(2,3).双曲线
的坐标为(2,3).双曲线 的图像经过BC的中点D,且与AB交于点E,连接DE.
的图像经过BC的中点D,且与AB交于点E,连接DE.
(1)求k的值及点E的坐标;
(2)若点F是边上一点,且ΔFCB∽ΔDBE,求直线FB的解析式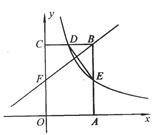
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知反比例函数y= (m为常数)的图象经过点A(-1,6).
(m为常数)的图象经过点A(-1,6).
(1)求m的值;
(2)如图,过点A作直线AC与函数y= 的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.
的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知反比例函数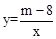 (m为常数)的图象经过点A(-1,6).
(m为常数)的图象经过点A(-1,6).
(1)求m的值;
(2)如图,过点A作直线AC与函数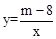 的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.
的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,直线 与双曲线
与双曲线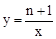 交于C、D两点,与x轴交于点A.
交于C、D两点,与x轴交于点A.
(1)求n的取值范围和点A的坐标;
(2)过点C作CB⊥y轴,垂足为B,若S △ABC=4,求双曲线的解析式;
(3)在(1)、(2)的条件下,若AB= ,求点C和点D的坐标并根据图象直接写出反比例函数的值小于一次函数的值时,自变量x的取值范围.
,求点C和点D的坐标并根据图象直接写出反比例函数的值小于一次函数的值时,自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com