
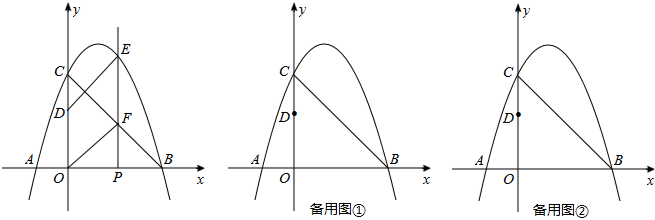
���� ��1�����ݴ���ϵ������ü��ɣ�
��2����P��m��0������E��m��-m2+2m+3�������PE=-m2+2m+3�����ݴ���ϵ�������ֱ��BC�Ľ���ʽ�����F�����꣬���PF=-m+3���������EF=-m2+3m������ƽ���ı��ε����ʵ�-m2+3m=2���Ӷ����P������ꣻ
��3���ȸ���B��C���������BC�ij���Ȼ����������Ӧ�ù��ɶ����������M�������꣬�������M�����꣮
��� 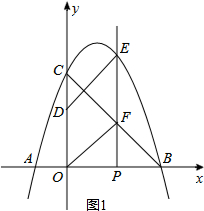 �⣺��1����������y=ax2+bx+3��x���ཻ�ڵ�A��-1��0����B��3��0����
�⣺��1����������y=ax2+bx+3��x���ཻ�ڵ�A��-1��0����B��3��0����
��$\left\{\begin{array}{l}{a-b+3=0}\\{9a+3b+3=0}\end{array}\right.$
���$\left\{\begin{array}{l}{a=-1}\\{b=2}\end{array}\right.$��
�������ߵĽ���ʽΪy=-x2+2x+3��
��2����ͼ1����P��m��0����
�ߵ�E���������ϵĵ㣬
��E��m��-m2+2m+3����
��PE=-m2+2m+3��
��x=0����y=-x2+2x+3�ã�y=3��
��C��0��3����
��ֱ��BC�Ľ���ʽΪy=kx+b��
��$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$��
����BC�Ľ���ʽΪy=-x+3��
�ߵ�F��ֱ��BC�ϣ�
��PF=-m+3
��EF=PE-PF=-m2+2m+3-��-m+3��=-m2+3m��
���ı���ODEF��ƽ���ı��Σ���EF=OD=2��
��-m2+3m=2��
��ã�m1=1��m2=2��
�൱�ı���ODEF��ƽ���ı���ʱ����P������Ϊ��1��0����2��0����
��3�����ڣ�
���ɣ���ͼ2���������ߵĽ���ʽΪy=-x2+2x+3��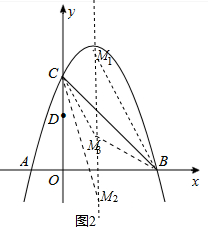
��Գ���x=-$\frac{2}{2����-1��}$=1��
��B��3��0����C��0��3����
��BC=$\sqrt{O{B}^{2}+O{C}^{2}}$=3$\sqrt{2}$��
��M��ֱ��x=1�ϣ�
����M��1��n����
�ٵ�BM=BC=3$\sqrt{2}$��
�ࣨ3-1��2+��0-n��2=��3$\sqrt{2}$��2��
��n=$\sqrt{14}$����n=-$\sqrt{14}$��
�ڵ�CM=BC=3$\sqrt{2}$��
��12+��3-n��2=��3$\sqrt{2}$��2��
��n=3+$\sqrt{17}$����n=3-$\sqrt{17}$��
�۵�CM=BMʱ��
�ࣨ3-1��2+��0-n��2=12+��3-n��2��
��n=1��
���ϣ�M�������Ϊ��1��$\sqrt{14}$����1��-$\sqrt{14}$����1��3+$\sqrt{17}$����1��3-$\sqrt{17}$����1��1����
���� �����Ƕ��κ������ۺ��⣬�����˴���ϵ���������ʽ�Լ�����ʽ�ĶԳ��ᣬ���ɶ�����Ӧ���Լ����������ε����ʵȣ����ݵ���������ݺ����Ľ���ʽ�����Ӧ��������DZ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
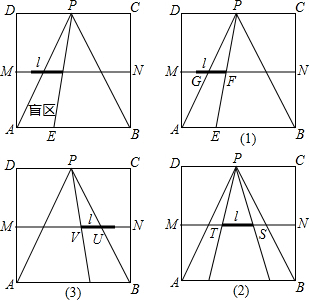
 �ס�����������ͬ��·����A�ص�B������ǰ����A��B���ؼ��·��Ϊ20km������ǰ����·��Ϊs��km�����׳������ʱ��Ϊt��h�����ס���ǰ����·����ʱ��ĺ���ͼ����ͼ��ʾ������ͼ����Ϣ������˵����ȷ����Ϊ��������
�ס�����������ͬ��·����A�ص�B������ǰ����A��B���ؼ��·��Ϊ20km������ǰ����·��Ϊs��km�����׳������ʱ��Ϊt��h�����ס���ǰ����·����ʱ��ĺ���ͼ����ͼ��ʾ������ͼ����Ϣ������˵����ȷ����Ϊ��������| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com