Question

7．如图示，若△ABC内一点P满足∠PAC=∠PBA=∠PCB，则点P为△ABC的布洛卡点．三角形的布洛卡点（Brocard  point）是法国数学家和数学教育家克洛尔（A．L．Crelle  1780-1855）于1816年首次发现，但他的发现并未被当时的人们所注意，1875年，布洛卡点被一个数学爱好者法国军官布洛卡（Brocard   1845-1922）重新发现，并用他的名字命名．问题：已知在等腰直角三角形DEF中，∠EDF=90°，若点Q为△DEF的布洛卡点，DQ=1，则EQ+FQ=（　　）

• A． 5
• B． 4
• C． $3+\sqrt{2}$
• D． $2+\sqrt{2}$

Answer 1

分析 由△DQF∽△FQE，推出$\frac{DQ}{FQ}$=$\frac{FQ}{QE}$=$\frac{DF}{EF}$=$\frac{1}{\sqrt{2}}$，由此求出EQ、FQ即可解决问题．

解答 解：如图，在等腰直角三角形△DEF中，∠EDF=90°，DE=DF，∠1=∠2=∠3，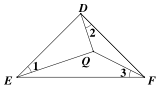

∵∠1+∠QEF=∠3+∠DFQ=45°，
∴∠QEF=∠DFQ，∵∠2=∠3，
∴△DQF∽△FQE，
∴$\frac{DQ}{FQ}$=$\frac{FQ}{QE}$=$\frac{DF}{EF}$=$\frac{1}{\sqrt{2}}$，
∵DQ=1，
∴FQ=$\sqrt{2}$，EQ=2，
∴EQ+FQ=2+$\sqrt{2}$，
故选D

点评 本题考查等腰直角三角形的性质、相似三角形的判定和性质等知识，解题的关键是正确寻找相似三角形解决问题，属于中考常考题型．