
【题目】已知抛物线![]()
抛物线 | 顶点坐标 | 与x轴交点坐标 | 与y轴交点坐标 | |
抛物线 | A(____) | B(____) | (1,0) | (0,-3) |
(1)补全表中A,B两点的坐标,并在所给的平面直角坐标系中,画出抛物线![]()
(2)结合图象回答
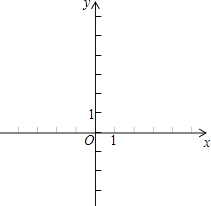
①当x的取值范围为________时,y随x的增大而增大;
②当x________时,![]() ;
;
③当![]() 时,y的取值范围________.
时,y的取值范围________.
【答案】(1)详见解析 (2) ①x>-1 ②x<-3或x>1 ③-4≤y<0
【解析】
(1)将函数解析式写成顶点式,可得出顶点坐标;一元二次方程x2+2x-3=0的解就是图象与x轴交点的横坐标;根据已知点画出函数图象即可.
(2)结合图象直接写出x或y的取值范围.
解:(1)∵y=x2+2x-3=x2+2x+1-4=(x+1)2-4
∴顶点坐标A(-1,-4).
∵x2+2x-3=0
解得:x1=1,x2=-3
∴与x轴交点坐标为(1,0)和(-3,0)
∴点B的坐标为(-3,0).
∴抛物线y=x2+2x-3图象如下:

(2)①∵图象开口向上,对称轴是x=-1,对称轴右侧递增
∴x>-1时,y随x的增大而增大.
②由图可以看出,x<-3或x>1时,y>0.
③由图可以看出,当-3<x<0时,-4≤y<0.
故答案为:(1)A(-1,-4)、B(-3,0);(2) ①x>-1; ② x<-3或x>1; ③-4≤y<0


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线![]() ,
,
![]() 求抛物线与
求抛物线与![]() 轴的交点坐标;
轴的交点坐标;
![]() 求抛物线与
求抛物线与![]() 轴的两个交点及两个交点间的距离.
轴的两个交点及两个交点间的距离.
![]() 求抛物线与
求抛物线与![]() 轴的交点及与
轴的交点及与![]() 轴交点所围成的三角形面积.
轴交点所围成的三角形面积.
![]() 把抛物线
把抛物线![]() 改为顶点式,说明顶点和对称轴.
改为顶点式,说明顶点和对称轴.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF ∥BC交AB于E,交AC于F,过点G作GD⊥ AC于D,下列四个结论:①EF = BE+CF;②∠BGC= 90 °+![]() ∠A;③点G到△ ABC各边的距离相等;④设GD =m,AE + AF =n,则S△AEF=
∠A;③点G到△ ABC各边的距离相等;④设GD =m,AE + AF =n,则S△AEF=![]() mn.其中正确的结论有( )
mn.其中正确的结论有( )

A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
材料一:数学上有一种根号内又带根号的数,它们能通过完全平方式及二次根式的性质化去一层(或多层)根号,如:![]()
材料二:配方法是初中数学思想方法中的一种重要的解题方法,配方法的最终目的就是配成完全平方式, 利用完全平方式来解决问题,它的应用非常广泛,在解方程、化简根式、因式分解等方面都经常 用到.
如:![]()
∵![]() ,∴
,∴![]() ,即
,即![]()
∴![]() 的最小值为
的最小值为![]()
阅读上述材料解决下面问题:
(1)![]() ,
,![]() ;
;
(2)求![]() 的最值;
的最值;
(3)已知![]() ,求
,求![]() 的最值.
的最值.
查看答案和解析>>
科目:初中数学 来源: 题型:
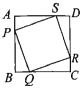
【题目】如图,![]() 四个小球分别从正方形的四个顶点
四个小球分别从正方形的四个顶点![]() 处出发(小球的大小忽略不计),以同样的速度分别沿
处出发(小球的大小忽略不计),以同样的速度分别沿![]() 方向滚动,其终点分别是点
方向滚动,其终点分别是点![]() ,顺次连接四个小球所在的位置,得到四边形
,顺次连接四个小球所在的位置,得到四边形![]() .
.
(1)不论小球滚动多长时间,求证;四边形![]() 总是正方形;
总是正方形;
(2)这个四边形在什么时候面积最大?
(3)在什么时侯四边形![]() 的面积为正方形
的面积为正方形![]() 面积的一半?请说明理由.
面积的一半?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市近郊有一块长为60米,宽为50米的矩形荒地,地方政府准备在此建一个综合性休闲广场,其中阴影部分为通道,通道的宽度均相等,中间的三个矩形(其中三个矩形的一边长均为a米)区域将铺设塑胶地面作为运动场地.设通道的宽度为x米.

(1)a= (用含x的代数式表示);
(2)若塑胶运动场地总占地面积为 2430平方米,则通道的宽度为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
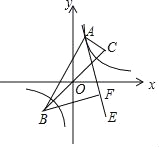
【题目】如图,点A是函数y=![]() 图象上的一点,已知B(﹣
图象上的一点,已知B(﹣![]() ,﹣
,﹣![]() ),C(
),C(![]() ,
,![]() ).试利用性质:“y=
).试利用性质:“y=![]() 图象上的任意一点P都满足|PB﹣PC|=2
图象上的任意一点P都满足|PB﹣PC|=2![]() ”求解下面问题:作∠BAC的内角平分线AE,过B作AE的垂线交AE于F.当点A在函数y=
”求解下面问题:作∠BAC的内角平分线AE,过B作AE的垂线交AE于F.当点A在函数y=![]() 图象上运动时,点F也总在一图形上运动,该图形为( )
图象上运动时,点F也总在一图形上运动,该图形为( )
A. 圆 B. 双曲线 C. 抛物线 D. 直线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是甲、乙两名同学近五次数学测试(满分均为100分)的成绩统计表:
同学 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次 |
甲 | 90 | 88 | 92 | 94 | 91 |
乙 | 90 | 91 | 93 | 94 | 92 |
根据上表数据,成绩较好且比较稳定的同学是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com