
【题目】已知:如图,AD是△ABC的中线,E为AD的中点,过点A作AF∥BC交BE延长线于点F,连接CF.
(1)如图1,求证:四边形ADCF是平行四边形;
(2)如图2,连接CE,在不添加任何辅助线的情况下,请直接写出图2中所有与△BDE面积相等的三角形.

【答案】(1)证明见解析;(2)△AEF、 △ABE、 △ACE 、△CDE.
【解析】
(1)证明△AEF≌△DEB,可得AF=DB,再根据 BD=CD可得AF=CD,再由AF//CD,根据有一组对边平行且相等的四边形是平行四边形即可证得结论;
(2)根据三角形中线将三角形分成面积相等的两个三角形以及全等三角形的面积相等即可得.
(1)![]() D为BC的点、E为AD的中点
D为BC的点、E为AD的中点
![]() BD=CD、AE=DE
BD=CD、AE=DE
![]() AF∥BC,
AF∥BC,
∴∠AFE=∠DBE,
在△AEF和△DEB中
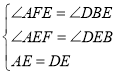 ,
,
∴△AEF≌△DEB,
∴AF=DB,
又∵ BD=CD
∴AF=CD,
又![]() AF∥BC,
AF∥BC,
∴四边形ADCF是平行四边形;
(2)∵△AEF≌△DEB,
∴S△AEF=S△DEB,
∵D为BC中点,
∴S△CDE=S△DEB,
∵E为AD中点,
∴S△ABE=S△DEB,S△ACE= S△CDE=S△DEB,
综上,与△BDE面积相等的三角形有△AEF、 △ABE、 △ACE 、△CDE.


科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫格点,网格中有以格点A、B、C为顶点的△ABC,请你根据所学的知识回答下列问题:

(1)求△ABC的面积;(2)判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课堂上,老师在黑板上出了一道题:在同一平面内,若∠AOB=70°,∠BOC=15°24′36″,求∠AOC的度数.
下面是七年级同学小明在黑板上写的解题过程:
解:根据题意可画出图(如图1)
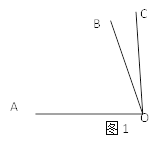
因为∠AOB=70°,∠BOC=15°24′36″,
所以∠AOC=∠AOB+∠BOC
=70°+15°24′36″
=85°24′36″
即得到∠AOC=85°24′36″
同学们在下面议论,都说小明解答不全面,还有另一种情况.请按下列要求完成这道题的求解.
(1)依照图1,用尺规作图的方法将另一种解法的图形在图2中补充完整.
(2)结合第(1)小题的图形写出求∠AOC的度数的完整过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
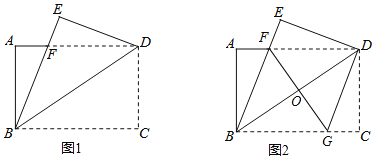
【题目】如图1,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,折线ABCDE描述了一汽车在某一直路上行驶时汽车离出发地的距离s(千米)和行驶时间t(小时)间的变量关系,则下列结论正确的是( )
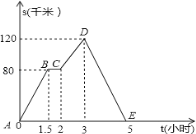
A. 汽车共行驶了120千米
B. 汽车在行驶途中停留了2小时
C. 汽车在整个行驶过程中的平均速度为每小时24千米
D. 汽车自出发后3小时至5小时间行驶的速度为每小时60千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民用水实行阶梯水价,实施细则如下表:
分档水量 | 年用水量 (立方米) | 水价 (元/立方米) |
第一阶梯 | 0~180(含) | 5.00 |
第二阶梯 | 181~260(含) | 7.00 |
第三阶梯 | 260以上 | 9.00 |
例如,某户家庭年使用自来水200 m3,应缴纳:180×5+(200-180)×7=1040元;
某户家庭年使用自来水300 m3,应缴纳:180×5+(260-180)×7+(300-260)×9=1820元.
(1)小刚家2017年共使用自来水170 m3,应缴纳 元;小刚家2018年共使用自来水260 m3,应缴纳 元.
(2)小强家2018年使用自来水共缴纳1180元,他家2018年共使用了多少自来水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. 若|a|=﹣a,则 a 一 定是负数
B. 单项式 x3y2z 的系数为 1,次数是 6
C. 若 AP=BP,则点 P 是线段 AB 的中点
D. 若∠AOC=![]() ∠AOB,则射线 OC 是∠AOB 的平分线
∠AOB,则射线 OC 是∠AOB 的平分线
查看答案和解析>>
科目:初中数学 来源: 题型:
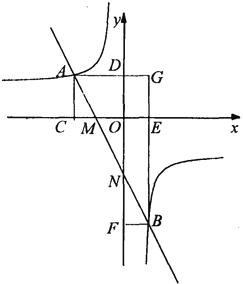
【题目】直线MN与x轴、y轴分别交于点M、N,并且经过第二、三、四象限,与反比例函数y=![]() (k<0)的图象交于点A、B,过A、B两点分别向x轴、y轴作垂线,垂足为C、D、E、F,AD与BF交于G点.
(k<0)的图象交于点A、B,过A、B两点分别向x轴、y轴作垂线,垂足为C、D、E、F,AD与BF交于G点.
(1)比较大小:S矩形ACOD S矩形BEOF(填“>,=,<”).
(2)求证:①AGGE=BFBG;
②AM=BN;
(3)若直线AB的解析式为y=﹣2x﹣2,且AB=3MN,则k的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某日的钱塘江观潮信息如图:

按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离s(千米)与时间t(分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点A(0,12),点B坐标为(m,0),曲线BC可用二次函数s=![]() t2+bt+c(b,c是常数)刻画.
t2+bt+c(b,c是常数)刻画.
(1)求m的值,并求出潮头从甲地到乙地的速度;
(2)11:59时,小红骑单车从乙地出发,沿江边公路以0.48千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为0.48千米/分,小红逐渐落后.问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度v=v0+![]() (t﹣30),v0是加速前的速度).
(t﹣30),v0是加速前的速度).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com