练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

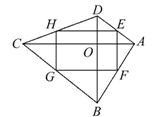
    如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为　　　　.


    12

    【解析】∵点E,F分别为四边形ABCD的边AD,AB的中点,∴EF∥BD,且EF=BD=3.

    同理求得GH∥BD,且GH=BD=3,EH∥AC∥GF,且EH=GF=AC=4,

    ∴四边形EFGH为平行四边形.

    又∵AC⊥BD,∴EF⊥FG.

    ∴四边形EFGH是矩形.

    ∴四边形EFGH的面积=EF·EH=3×4=12,

    即四边形EFGH的面积是12.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    某水果批发市场香蕉的价格如表:

    购买香蕉数

    (kg)

    不超过

    20kg

    20kg以上

    但不超过40kg

    40kg

    以上

    每kg价格

    8元

    7元

    6元

    若小强购买香蕉xkg(x大于40kg)付了y元,则y关于x的函数解析式为　　　　　　　　.(写出自变量的取值范围)

    查看答案和解析>>

    科目：初中数学 来源： 题型：


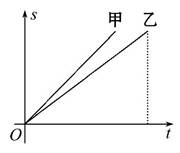    甲、乙两人在一次百米赛跑中,路程s(m)与赛跑时间t(s)的关系如图所示,则下列说法正确的是(　　)

    A.甲、乙两人的速度相同

    B.甲先到达终点

    C.乙用的时间短

    D.乙比甲跑的路程多

    查看答案和解析>>

    科目：初中数学 来源： 题型：


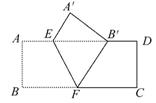
    如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B'处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是(　　)

    A.12            B.24            C.12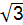         D.16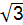

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    阅读以下短文,然后解决下列问题:

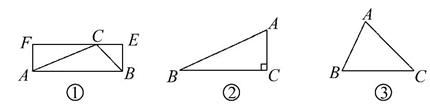
    如果一个三角形和一个矩形满足条件:三角形的一边与矩形的一边重合,且三角形的这边所对的顶点在矩形这边的对边上,则称这样的矩形为三角形的“友好矩形”.如图①所示,矩形ABEF即为△ABC的“友好矩形”.显然,当△ABC是钝角三角形时,其“友好矩形”只有一个.

    (1)仿照以上叙述,说明什么是一个三角形的“友好平行四边形”.

    (2)如图②,若△ABC为直角三角形,且∠C=90°,在图②中画出△ABC的所有“友好矩形”,并比较这些矩形面积的大小.

    (3)若△ABC是锐角三角形,且BC>AC>AB,在图③中画出△ABC的所有“友好矩形”,指出其中周长最小的矩形并加以证明.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件中能够判定四边形ACED为菱形的是(　　)

    A.AB=BC             B.AC=BC

    C.∠B=60°          D.∠ACB=60°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


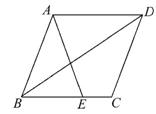
    如图,在平行四边形ABCD中,E为BC边上的一点,连接AE,BD且AE=AB.

    (1)求证:∠ABE=∠EAD.

    (2)若∠AEB=2∠ADB,求证:四边形ABCD是菱形.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知正比例函数y=kx(k是常数,k≠0),当-3≤x≤1时,对应的y的取值范围是-1≤y≤,且y随x的减小而减小,求k的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    有5个从小到大排列的正整数,中位数是3,唯一的众数是8,则这5个数的和为　　　　.

    查看答案和解析>>

    同步练习册答案