
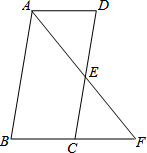
 如图,在?ABCD中,点E是DC的中点,连接AE,并延长交BC的延长线于点F.
如图,在?ABCD中,点E是DC的中点,连接AE,并延长交BC的延长线于点F.分析 (1)首先根据平行四边形的性质可得AD∥BC,根据平行线的性质可得∠DAE=∠F,然后再证明△AED≌△FEC可得结论;
(2)首先根据平行四边形的性质可得AD=BC,根据全等三角形的性质可得AD=CF,然后再证明AB=BF,进而可得∠BAF=∠F,再由∠DAE=∠F,可得∠BAF=∠DAE,进而可得AF恰好是∠BAD的平分线.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠F,
∵点E是DC的中点,
∴CE=DE,
在△AED和△FEC中$\left\{\begin{array}{l}{∠DAE=∠F}\\{∠AED=∠CEF}\\{DE=CE}\end{array}\right.$,
∴△AED≌△FEC(AAS),
∴△ADE和△CEF的面积相等;
(2)∵四边形ABCD是平行四边形,
∴AD=BC,
∵△AED≌△FEC,
∴AD=CF,
∴AD=BC=CF,
∵AB=2AD,
∴AB=2BC=BF,
∴∠BAF=∠F,
又∵∠DAE=∠F,
∴∠BAF=∠DAE,
即AF是∠BAD的平分线.
点评 此题主要考查了平行四边形的性质以及全等三角形判定和性质,关键是掌握平行四边形的对边相等,对边平行.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:解答题
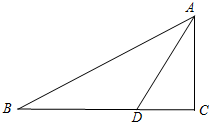 已知在Rt△ABC中,AC⊥BC,AD是∠BAC的角分线,以AB上的一点O为圆心,AD为弦作⊙O.
已知在Rt△ABC中,AC⊥BC,AD是∠BAC的角分线,以AB上的一点O为圆心,AD为弦作⊙O.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 年龄组 | 12岁 | 13岁 | 14岁 | 15岁 |
| 参赛人数 | 5 | 20 | 12 | 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12 | B. | 16 | C. | 16或20 | D. | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 一辆汽车和一辆摩托车分别从A,B两地去同一个城市,它们离A地的路程随时间变化的图象如图所示.则下列结论:(1)摩托车比汽车晚到1h;(2)A,B两地的路程为20km;(3)摩托车的速度为45km/h,汽车的速度为60km/h;(4)汽车出发1小时候与摩托车相遇,此时距B地40千米;(5)相遇前摩托车的速度比汽车的速度慢.其中正确结论的个数是( )
一辆汽车和一辆摩托车分别从A,B两地去同一个城市,它们离A地的路程随时间变化的图象如图所示.则下列结论:(1)摩托车比汽车晚到1h;(2)A,B两地的路程为20km;(3)摩托车的速度为45km/h,汽车的速度为60km/h;(4)汽车出发1小时候与摩托车相遇,此时距B地40千米;(5)相遇前摩托车的速度比汽车的速度慢.其中正确结论的个数是( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
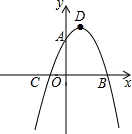 如图,抛物线y=ax2-2ax-3a交y轴于A点,交x轴于B,C两点(B在C右边),顶点为D.
如图,抛物线y=ax2-2ax-3a交y轴于A点,交x轴于B,C两点(B在C右边),顶点为D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
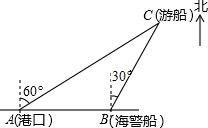 一艘观光游船从港口A以北偏东60°的方向出港观光,航行60海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东30°方向,马上以40海里每小时的速度前往救援,海警船到达事故船C处所需的时间大约为$\frac{\sqrt{3}}{2}$小时(用根号表示).
一艘观光游船从港口A以北偏东60°的方向出港观光,航行60海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东30°方向,马上以40海里每小时的速度前往救援,海警船到达事故船C处所需的时间大约为$\frac{\sqrt{3}}{2}$小时(用根号表示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 应试者 | 计算机技能 | 语言表达 | 商品知识 |
| 甲 | 70 | 50 | 80 |
| 乙 | 90 | 75 | 45 |
| 丙 | 50 | 60 | 85 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com